图神经网络和GCN

图神经网络

为什么使用图神经网络

传统神经网络（如CNN、RNN）难以直接处理非欧几里得结构数据（图结构数据）（如社交网络、分子结构）。现实世界中的许多数据都可以表示为图结构，如社交网络、生物网络、知识图谱、分子结构等，图神经网络能够直接对图结构数据进行建模，自动学习节点之间的复杂关系和依赖，捕捉数据中的全局和局部结构信息。

图神经网络的引入

对于一个图结构，其中包含了许多节点和边，我们认为每个节点并不是独立的，节点都会受到其他节点（比如相邻节点）的影响。

消息传递机制（Message Passing）：每个节点通过聚合邻居的信息，并结合自身的特征，生成新的节点表示。这一过程模仿了现实中的信息传播（如社交网络中观点扩散、分子中原子的相互作用）。

消息传递的三个步骤：

  1. 消息生成（Message）：邻居节点向目标节点发送信息。

  2. 聚合（Aggregation）：目标节点将收到的所有邻居信息汇总。

  3. 更新（Update）：目标节点结合聚合后的信息和自身特征，生成新表示。

以第\(k\)层GNN的节点\(v\)为例，其更新过程如下：

  1. 消息生成：

    邻居节点\(u\in\mathcal{N}(v)\)，向\(v\)发送消息： \[ \mathbf{m}_{u\rightarrow v}^{(k)} = \mathrm{Message}\left(\mathbf{h}_u^{(k-1)}, \mathbf{h}_v^{(k-1)}, e_{uv}\right) \]

    • \(\mathbf{h}_u^{(k-1)}\)：邻居节点\(u\)的上一层的特征向量
    • \(e_{uv}\)：边\(u\rightarrow v\)的特征（如权重、类型）
    • \(\mathrm{Message}()\)：消息函数，通常是一个可学习的神经网络（如MLP）或简单线性变换

  2. 聚合：

    目标节点\(v\)将所有邻居消息汇总： \[ \mathbf{m}_v^{(k)} = \mathrm{Aggregate\left(\set{\mathbf{m}_{u\rightarrow v}^{(k)}\ | \ u\in\mathcal{N}(v)}\right)} \]

    • \(\mathrm{Aggregate}()\)：聚合函数，常见方式包括：
      • 求和（Sum）：捕捉邻居信息的累加效应（如分子中原子的总电荷）
      • 均值（Mean）：均衡各邻居贡献，防止度数高的节点主导
      • 最大值（Max）：关注最显著的特征（如社交网络中的关键意见领袖）
      • 注意力加权（Attention）：动态学习邻居重要性

  3. 更新：

    结合聚合后的消息\(\mathbf{m}_v^{(k)}\)和节点自身特征\(\mathbf{h}_v^{(k-1)}\)，生成新的特征： \[ \mathbf{h}_v^{(k)} = \mathrm{Update}\left(\mathbf{h}_v^{(k-1)}, \mathbf{m}_v^{(k)}\right) \]

    • \(\mathrm{Update}()\)：更新函数，常用门控机制（如GRU）或全连接层。

注意：图神经网络的一层指的是一层的邻居，而不是消息生成或者更新中可学习网络（如MLP）的层数，比如，对于当前的节点\(v\)，第一层就是指\(v\)的邻居，第二层就是指\(v\)邻居的邻居（第一层聚合了节点的邻居，第二层中因为当前节点包含了邻居节点的信息，邻居节点也包含了其邻居节点的信息，因此可以看为聚合了邻居的邻居）。

图神经网络在多层堆叠后，容易出现过度平滑（Over-smoothing）的现象，即所有的特征趋于相似。为了解决这个问题，可以引入残差连接（Residual Connection）、跳跃连接（Jumping Knowledge）等。

图神经网络中，每个节点对应一个输出，因此可以将每个节点看做一个样本。每个节点的输出可以用于对节点的分类等任务。

GCN

引入

GCN，图卷积网络（Graph Convolution Network），是图神经网络中最简单的一种，原理就是聚合邻居的特征，通过非线性变换，得到自己的新特征（在GCN中并未考虑边的特征）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import torch
import torch.nn as nn

class GCNLayer(nn.Module):
    def __init__(self, input_dim, output_dim):
        super().__init__()
        self.linear = nn.Linear(input_dim, output_dim)
        
    def forward(self, x, edge_index):
        """
        x: 节点特征, [num_nodes, input_dim], 即每行是一个节点的特征，输入特征维度为input_dim
        edge_index: 边的索引, [2, num_edges], 第一行为所有边的源节点(source node)索引，第二行为所有边的目标节点(target node)索引，每一列表示一条边
        """
        # 聚合邻居信息（求和）
        neighbor_msg = torch.zeros_like(x)	# [num_nodes, input_dim]
        
        for src, dst in edge_index.t():
            neighbor_msg[dst] += x[src]
            
        # 更新节点特征
        x = self.linear(x + neighbor_msg)	# [num_nodes, output_dim]
        return torch.relu(x)
    
class GNN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super().__init__()
        self.layer1 = GNNLayer(input_dim, hidden_dim)	# 第一层
        self.layer2 = GNNLayer(hidden_dim, output_dim)	# 第二层
        
    def forward(self, x, edge_index):
        x = self.layer1(x, edge_index)	# 第一层：直接聚合邻居
        x = self.layer2(x, edge_index)	# 第二层：聚合邻居的邻居
        return x

上面的代码实现了GCN的模型，但是存在一个很大的问题，就是无法充分利用GPU资源进行训练，for循环会在每条边聚合一次信息，如果图比较大，那么运行就会非常慢。

下面引入可以在GPU上并行训练的GCN模型，包含公式、推导及实现。

GCN公式及推导

公式

\[ \mathbf{H}^{(k+1)} = \sigma(\tilde{\mathbf{D}}^{-\frac{1}{2}}\tilde{\mathbf{A}}\tilde{\mathbf{D}}^{-\frac{1}{2}}\mathbf{H}^{(k)}\mathbf{W}^{(k)}) \]

\[ \begin{aligned} &\tilde{\mathbf{D}} = \mathbf{D} + \mathbf{I} &\tilde{\mathbf{A}} = \mathbf{A} + \mathbf{I} \end{aligned} \]

其中，\(\mathbf{A}\in\mathbb{R}^{|V|\times|V|}\)是邻接矩阵，其中第\(i\)行第\(j\)列的元素\(a_{ij}\)表示的是节点\(i\)与节点\(j\)是否有边相连（\(a_{ij}=1\)代表有边相连，\(a_{ij}=0\)代表无边相连）。\(V\)是图中的所有节点的集合，\(|V|\)是所有节点的个数。\(\mathbf{D}\in\mathbb{R}^{|V|\times|V|}\)是度矩阵，是对角阵，其中第\(i\)行第\(i\)列的元素\(d_i\)表示的是第\(i\)个节点的度（相邻节点的个数）。\(\mathbf{I}\in\mathbb{R}^{|V|\times|V|}\)是单位阵。\(\mathbf{H}^{(k)}\)是各节点的在GCN第\(k\)层的嵌入向量，满足： \[ \begin{aligned} \mathbf{H}^{(k)} &= \left[\begin{matrix}\mathbf{h}_1^{(k)}&\cdots&\mathbf{h}_{|V|}^{(k)}\end{matrix}\right]^\top\\ &= \left[ \begin{matrix} {\mathbf{h}_1^{(k)}}^\top\\ {\mathbf{h}_2^{(k)}}^\top\\ \vdots\\ {\mathbf{h}_{|V|}^{(k)}}^\top \end{matrix} \right] \end{aligned} \] 其中\(\mathbf{h}_i^{(k)}\)表示的是第\(i\)个节点在GCN第\(k\)层的嵌入向量，此处为列向量。

推导

\[ \begin{aligned} \mathbf{H}^{(k)} &= \left[\begin{matrix}\mathbf{h}_1^{(k)}&\cdots&\mathbf{h}_{|V|}^{(k)}\end{matrix}\right]^\top\\ &= \left[ \begin{matrix} {\mathbf{h}_1^{(k)}}^\top\\ {\mathbf{h}_2^{(k)}}^\top\\ \vdots\\ {\mathbf{h}_{|V|}^{(k)}}^\top \end{matrix} \right] \end{aligned} \]

其中\(V\)是所有的节点的集合，\(|V|\)是所有节点的数量，\(\mathrm{h}_i^{(k)}\)是第\(k\)层第\(i\)节点的嵌入向量（为列向量），\(\mathrm{H}^{(k)}\)是所有节点嵌入向量构成的矩阵。

\(\mathbf{A}\)为邻接矩阵，其中第\(i\)行第\(j\)列\(a_{ij}\)为1代表节点\(i\)与节点\(j\)有边，\(a_{ij}=0\)代表节点\(i\)与节点\(j\)无边。邻接矩阵\(\mathbf{A}\)的第\(i\)行\(\mathbf{A}_i\)代表节点\(i\)与哪些节点是有边的。

考虑邻接矩阵的第\(i\)行： \[ \mathbf{A}_i = \left[\begin{matrix}a_{i1}&a_{i2}&\cdots&a_{i,|V|}\end{matrix}\right] \] 则 \[ \begin{aligned} \mathbf{A}_i\mathbf{H}^{(k)} &= \left[ \begin{matrix} a_{i1}&a_{i2}&\cdots&a_{i,|V|} \end{matrix} \right]\cdot\left[ \begin{matrix} {\mathbf{h}_1^{(k)}}^\top\\ {\mathbf{h}_2^{(k)}}^\top\\ \vdots\\ {\mathbf{h}_{|V|}^{(k)}}^\top \end{matrix} \right]\\ \\ &= a_{i1}{\mathbf{h}_1^{(k)}}^\top + a_{i2}{\mathbf{h}_2^{(k)}}^\top + \cdots + a_{i,|V|}{\mathbf{h}_{|V|}^{(k)}}^\top\\ \\ &= \sum_{j=1}^{|V|}a_{i,j}{\mathbf{h}_j^{(k)}}^\top \end{aligned} \] 其中，\(a_{i,j} = 1\)（节点\(i\)与节点\(j\)有边，相邻）或\(a_{i,j} = 0\)（节点\(i\)与节点\(j\)无边，不相邻）

即\(\mathbf{A}_i\mathbf{H}^{(k)}\)代表与\(i\)相邻的节点的嵌入矩阵的和。

考虑整个邻接矩阵： \[ \mathbf{A} = \left[ \begin{matrix} \mathbf{A}_1\\ \mathbf{A}_2\\ \vdots\\ \mathbf{A}_{|V|} \end{matrix} \right] \] 则 \[ \begin{aligned} \mathbf{A}\mathbf{H}^{(k)} &= \left[ \begin{matrix} \mathbf{A}_1\\ \mathbf{A}_2\\ \vdots\\ \mathbf{A}_{|V|} \end{matrix} \right]\cdot\mathbf{H}^{(k)}\\ \\ &= \left[ \begin{matrix} \mathbf{A}_1\mathbf{H}^{(k)}\\ \mathbf{A}_2\mathbf{H}^{(k)}\\ \vdots\\ \mathbf{A}_{|V|}\mathbf{H}^{(k)} \end{matrix} \right]\\ \\ &= \left[ \begin{matrix} \sum_{j=1}^{|V|}a_{1,j}{\mathbf{h}_j^{(k)}}^\top\\ \sum_{j=1}^{|V|}a_{2,j}{\mathbf{h}_j^{(k)}}^\top\\ \vdots\\ \sum_{j=1}^{|V|}a_{|V|,j}{\mathbf{h}_j^{(k)}}^\top \end{matrix} \right] \end{aligned} \] 如果直接对相邻节点的嵌入向量直接求和，那么很可能导致结果变得很大，为了解决这个问题，先引入度矩阵： \[ \mathbf{D} = \left[ \begin{matrix} d_1&0&0&\cdots&0\\ 0&d_2&0&\cdots&0\\ 0&0&d_3&\cdots&0\\ \vdots&\vdots&\vdots& &\vdots\\ 0&0&0&\cdots&d_{|V|} \end{matrix} \right] \] 其中\(d_i\)表示与节点\(i\)相连的节点的个数，度矩阵\(\mathbf{D}\)是一个对角阵。

令\(\mathbf{D}^{-1}\)为\(\mathbf{D}\)中每个元素求倒数，\(\mathbf{D}^{\frac{1}{2}}\)为\(\mathbf{D}\)中每个元素开根号，\(\mathbf{D}^{-\frac{1}{2}}\)为\(\mathbf{D}\)中每个元素开根号之后求倒数： \[ \mathbf{D}^{-1} = \left[ \begin{matrix} \frac{1}{d_1}&0&0&\cdots&0\\ 0&\frac{1}{d_2}&0&\cdots&0\\ 0&0&\frac{1}{d_3}&\cdots&0\\ \vdots&\vdots&\vdots& &\vdots\\ 0&0&0&\cdots&\frac{1}{d_{|V|}} \end{matrix} \right] \]

\[ \mathbf{D}^{\frac{1}{2}} = \left[ \begin{matrix} \sqrt{d_1}&0&0&\cdots&0\\ 0&\sqrt{d_2}&0&\cdots&0\\ 0&0&\sqrt{d_3}&\cdots&0\\ \vdots&\vdots&\vdots& &\vdots\\ 0&0&0&\cdots&\sqrt{d_{|V|}} \end{matrix} \right] \]

\[ \mathbf{D}^{-\frac{1}{2}} = \left[ \begin{matrix} \frac{1}{\sqrt{d_1}}&0&0&\cdots&0\\ 0&\frac{1}{\sqrt{d_2}}&0&\cdots&0\\ 0&0&\frac{1}{\sqrt{d_3}}&\cdots&0\\ \vdots&\vdots&\vdots& &\vdots\\ 0&0&0&\cdots&\frac{1}{\sqrt{d_{|V|}}} \end{matrix} \right] \]

则： \[ \begin{aligned} \mathbf{D}^{-1}\mathbf{A} &= \left[ \begin{matrix} \frac{1}{d_1}&0&0&\cdots&0\\ 0&\frac{1}{d_2}&0&\cdots&0\\ 0&0&\frac{1}{d_3}&\cdots&0\\ \vdots&\vdots&\vdots& &\vdots\\ 0&0&0&\cdots&\frac{1}{d_{|V|}} \end{matrix} \right]\cdot\left[ \begin{matrix} a_{11}&a_{12}&a_{13}&\cdots&a_{1,|V|}\\ a_{21}&a_{22}&a_{23}&\cdots&a_{2,|V|}\\ a_{31}&a_{32}&a_{33}&\cdots&a_{3,|V|}\\ \vdots&\vdots&\vdots&&\vdots\\ a_{|V|,1}&a_{|V|,2}&a_{|V|,3}&\cdots&a_{|V|,|V|} \end{matrix} \right]\\ &= \left[ \begin{matrix} \frac{a_{11}}{d_1}&\frac{a_{12}}{d_1}&\frac{a_{13}}{d_1}&\cdots&\frac{a_{1,|V|}}{d_1}\\ \frac{a_{21}}{d_2}&\frac{a_{22}}{d_2}&\frac{a_{23}}{d_2}&\cdots&\frac{a_{2,|V|}}{d_2}\\ \frac{a_{31}}{d_3}&\frac{a_{32}}{d_3}&\frac{a_{33}}{d_3}&\cdots&\frac{a_{3,|V|}}{d_3}\\ \vdots&\vdots&\vdots&&\vdots\\ \frac{a_{|V|,1}}{d_{|V|}}&\frac{a_{|V|,2}}{d_{|V|}}&\frac{a_{|V|,3}}{d_{|V|}}&\cdots&\frac{a_{|V|,|V|}}{d_{|V|}} \end{matrix} \right]\\ &= \left[ \begin{matrix} \frac{1}{d_1}\mathbf{A}_1\\ \frac{1}{d_2}\mathbf{A}_2\\ \vdots\\ \frac{1}{d_{|V|}}\mathbf{A}_{|V|} \end{matrix} \right] \end{aligned} \]

可以得到： \[ \begin{aligned} \mathbf{D}^{-1}\mathbf{A}\mathbf{H}^{(k)} &= \left[ \begin{matrix} \frac{1}{d_1}\mathbf{A}_1\mathbf{H}^{(k)}\\ \frac{1}{d_2}\mathbf{A}_2\mathbf{H}^{(k)}\\ \vdots\\ \frac{1}{d_{|V|}}\mathbf{A}_{|V|}\mathbf{H}^{(k)} \end{matrix} \right]\\ &= \left[ \begin{matrix} \frac{1}{d_1}\sum_{j=1}^{|V|}a_{1,j}{\mathbf{h}_j^{(k)}}^\top\\ \frac{1}{d_2}\sum_{j=1}^{|V|}a_{2,j}{\mathbf{h}_j^{(k)}}^\top\\ \vdots\\ \frac{1}{d_{|V|}}\sum_{j=1}^{|V|}a_{|V|,j}{\mathbf{h}_j^{(k)}}^\top \end{matrix} \right] \end{aligned} \]

这样，对于该矩阵的每行，就是对对应节点的相连的节点的嵌入向量求平均值。

但这样做，会将每个相连的节点都看做同等重要，在GCN中，认为该节点\(i\)的所有连接节点\(j\)中，邻居数量越少的\(j\)节点的信息越重要，比如对于下面的图：

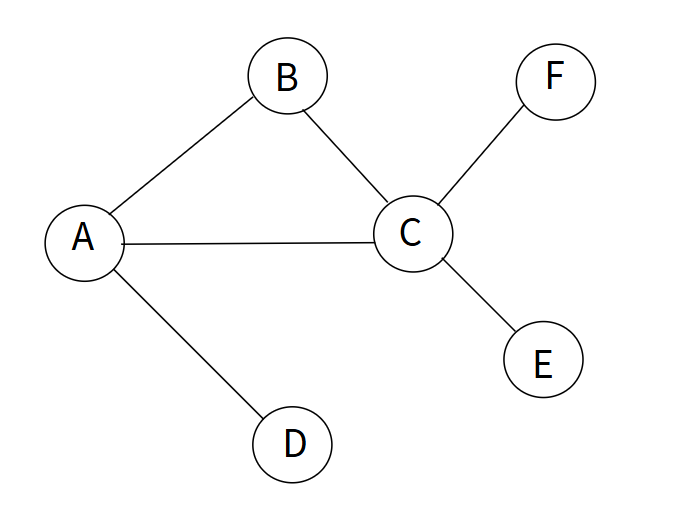
从两层GCN来看：

第二层：\(A\)的邻居节点有\(B\)、\(C\)、\(D\)

第一层：\(B\)的邻居节点有\(A\)、\(C\)；\(C\)的邻居节点有\(A\)、\(B\)、\(E\)、\(F\)；\(D\)的邻居节点有\(A\)

由于节点\(C\)与很多节点都相邻，那么其他很多节点都会考虑到\(C\)节点，节点\(C\)也会考虑到很多节点，也就是说，相邻节点数量多的节点，它的信息已经被很多节点在多层GCN传播的时候包含了，很多节点的信息在多层GCN传播的时候也已经被该节点包含了。而相邻节点数量少的节点，其包含其他节点的信息量则比较少，其他节点包含该节点的信息量也会比较少或者不包含该节点的信息。因此，从多层GCN的角度来看，如果仅仅只是对上一层的节点信息求平均，那么会包含更多的邻居数量多的节点的信息，包含更少的邻居数量少的节点的信息，GCN层数越多，这种情况会越明显，使得邻居数量少的节点信息占比越来越少。为了避免这个问题，在聚合相邻节点信息的时候，应该考虑到相邻节点的度（邻居个数），度越少的节点的信息越重要，因此我们可以对邻接矩阵\(\mathbf{A}\)的每列进行平均： \[ \begin{aligned} \mathbf{A}\mathbf{D}^{-1} &= \left[ \begin{matrix} a_{11}&a_{12}&a_{13}&\cdots&a_{1,|V|}\\ a_{21}&a_{22}&a_{23}&\cdots&a_{2,|V|}\\ a_{31}&a_{32}&a_{33}&\cdots&a_{3,|V|}\\ \vdots&\vdots&\vdots&&\vdots\\ a_{|V|,1}&a_{|V|,2}&a_{|V|,3}&\cdots&a_{|V|,|V|} \end{matrix} \right]\cdot\left[ \begin{matrix} \frac{1}{d_1}&0&0&\cdots&0\\ 0&\frac{1}{d_2}&0&\cdots&0\\ 0&0&\frac{1}{d_3}&\cdots&0\\ \vdots&\vdots&\vdots& &\vdots\\ 0&0&0&\cdots&\frac{1}{d_{|V|}} \end{matrix} \right] \\ &= \left[ \begin{matrix} \frac{a_{11}}{d_1}&\frac{a_{12}}{d_2}&\frac{a_{13}}{d_3}&\cdots&\frac{a_{1,|V|}}{d_{|V|}}\\ \frac{a_{21}}{d_1}&\frac{a_{22}}{d_2}&\frac{a_{23}}{d_3}&\cdots&\frac{a_{2,|V|}}{d_{|V|}}\\ \frac{a_{31}}{d_1}&\frac{a_{32}}{d_2}&\frac{a_{33}}{d_3}&\cdots&\frac{a_{3,|V|}}{d_{|V|}}\\ \vdots&\vdots&\vdots&&\vdots\\ \frac{a_{|V|,1}}{d_1}&\frac{a_{|V|,2}}{d_2}&\frac{a_{|V|<3}}{d_3}&\cdots&\frac{a_{|V|,|V|}}{d_{|V|}} \end{matrix} \right] \end{aligned} \] 则 \[ \mathbf{A}\mathbf{D}^{-1}\mathbf{H}^{(k)} = \left[ \begin{matrix} \sum_{j=1}^{|V|}\frac{1}{d_j}a_{1,j}{\mathbf{h}_j^{(k)}}^\top\\ \sum_{j=1}^{|V|}\frac{1}{d_j}a_{2,j}{\mathbf{h}_j^{(k)}}^\top\\ \vdots\\ \sum_{j=1}^{|V|}\frac{1}{d_j}a_{|V|,j}{\mathbf{h}_j^{(k)}}^\top \end{matrix} \right] \] 这样，邻居节点\(j\)的度越大，求和时其信息占比越小（权重为\(\frac{1}{d_j}\)），结合对所有信息的平均： \[ \mathbf{D}^{-1}\mathbf{A}\mathbf{D}^{-1}\mathbf{H}^{(k)} = \left[ \begin{matrix} \frac{1}{d_1}\sum_{j=1}^{|V|}\frac{1}{d_j}a_{1,j}{\mathbf{h}_j^{(k)}}^\top\\ \frac{1}{d_2}\sum_{j=1}^{|V|}\frac{1}{d_j}a_{2,j}{\mathbf{h}_j^{(k)}}^\top\\ \vdots\\ \frac{1}{d_{|V|}}\sum_{j=1}^{|V|}\frac{1}{d_j}a_{|V|,j}{\mathbf{h}_j^{(k)}}^\top \end{matrix} \right] \] 这样依旧有一个缺点：层数越多节点的数值越小，假设一个节点的嵌入向量的每个元素均满足标准正态分布\(\mathcal{N}(0,1)\)，易知\(\mathbf{D}^{-1}\mathbf{A}\mathbf{H}^{(k)}\)中的每个元素也会满足标准正态分布\(\mathcal{N}(0,1)\)，则\(\mathbf{D}^{-1}\mathbf{A}\mathbf{D}^{-1}\mathbf{H}^{(k)}\)中每个元素的均值为0，方差会比1更小，经过多层后，方差会越来越小，值会越来越接近于0。

如果既要考虑所求节点和其相邻节点的度，又要尽量保证聚合后各元素维持一个比较稳定的分布（均值和方差尽可能不变），就应该综合考虑： \[ \mathbf{D}^{-\frac{1}{2}}\mathbf{A}\mathbf{D}^{-\frac{1}{2}}\mathbf{H}^{(k)} = \left[ \begin{matrix} \frac{1}{\sqrt{d_1}}\sum_{j=1}^{|V|}\frac{1}{\sqrt{d_j}}a_{1,j}{\mathbf{h}_j^{(k)}}^\top\\ \frac{1}{\sqrt{d_2}}\sum_{j=1}^{|V|}\frac{1}{\sqrt{d_j}}a_{2,j}{\mathbf{h}_j^{(k)}}^\top\\ \vdots\\ \frac{1}{\sqrt{d_{|V|}}}\sum_{j=1}^{|V|}\frac{1}{\sqrt{d_j}}a_{|V|,j}{\mathbf{h}_j^{(k)}}^\top \end{matrix} \right] \] \(\mathbf{D}^{-\frac{1}{2}}\mathbf{A}\mathbf{D}^{-\frac{1}{2}}\mathbf{H}^{(k)}\)既考虑了对不同度的邻居节点的加权求和，又考虑了数值的稳定性。

上面的这个公式并没有考虑节点本身，而节点本身也是一个很重要的信息，因此，我们一般在图的节点上加入自环，使节点连接本身：

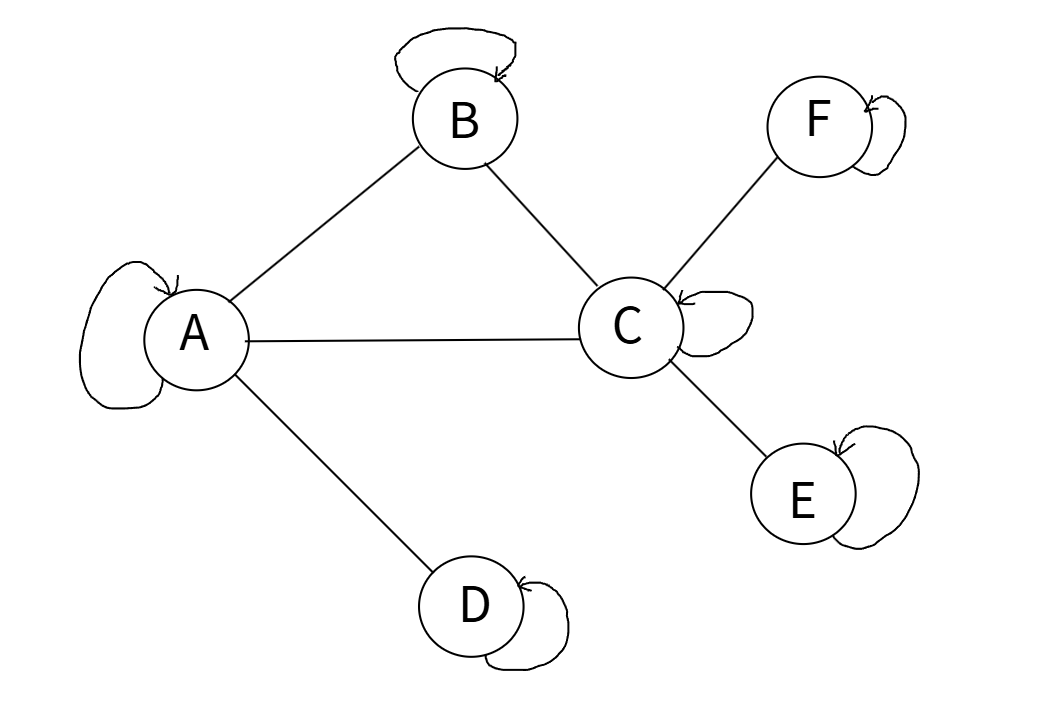
设单位矩阵\(\mathbf{I}\in\mathbb{R}^{|V|\times|V|}\)，新的邻接矩阵\(\tilde{\mathbf{A}}\)为： \[ \tilde{\mathbf{A}} = \mathbf{A} + \mathbf{I} \] 即相比于原先的邻接矩阵，新的邻接矩阵的第\(i\)行第\(i\)列为1，表示自己与自己相连。

那么每个节点的度也需要加一，新的度矩阵\(\tilde{\mathbf{D}}\)为： \[ \tilde{\mathbf{D}} = \mathbf{D} + \mathbf{I} \] 则，新的公式为： \[ \tilde{\mathbf{D}}^{-\frac{1}{2}}\tilde{\mathbf{A}}\tilde{\mathbf{D}}^{-\frac{1}{2}}\mathbf{H}^{(k)} \] 即对包含自己节点和邻居节点进行加权求和，聚合信息。

信息聚合后，通过神经网络的线性层和激活函数，得到每个节点新的嵌入向量： \[ \mathbf{H}^{(k+1)} = \sigma(\tilde{\mathbf{D}}^{-\frac{1}{2}}\tilde{\mathbf{A}}\tilde{\mathbf{D}}^{-\frac{1}{2}}\mathbf{H}^{(k)}\mathbf{W}^{(k)}) \] 其中，\(\mathbf{H}^{(k)}\in\mathbb{R}^{|V|\times d^{(k)}}\)，\(d^{(k)}\)为第\(k\)层各节点嵌入向量的维度；\(\mathbf{W}^{(k)}\in\mathbb{R}^{d^{(k)}\times d^{(k+1)}}\)，\(d^{(k+1)}\)为第\(k+1\)层各节点嵌入向量的维度，则\(\mathbf{H}^{(k+1)}\in\mathbb{R}^{|V|\times d^{(k+1)}}\)

实现

一层GCN结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import torch
import torch.nn as nn
import torch.nn.functional as F

class GraphConvolution(nn.Module):
    def __init__(self, in_features, out_features, bias=True):
        super().__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = nn.Parameters(torch.zeros(in_features, out_features))
        if bias:
            self.bias = nn.Parameters(torch.zeros(out_feaures))
        else:
            self.register_parameter('bias', None)
        self.reset_parameters()
        
    def reset_parameters(self):
        nn.init.xavier_uniform_(self.weight)
        if self.bias is not None:
            nn.init.zeros_(self.bias)
    
    def forward(self, input, adj):
        """
        input:节点的特征矩阵（嵌入向量） [N, F], 图中一共N个节点，每个节点的嵌入向量维度为F
        adj: 图的邻接矩阵 [N, N]
        """
        support = torch.mm(input, self.weight)
        output = torch.spmm(adj, support)
        if self.bias is not None:
            return output + self.bias
        else:
            return output

其中，torch.spmm()是PyTorch中专门用于执行稀疏矩阵和密集矩阵的乘法的函数。

图的邻接矩阵\(\mathbf{A}\)往往是稀疏矩阵，因为大部分节点之间不存在连接。稀疏矩阵包含大量的零元素，若使用常规的矩阵乘法（如torch.mm()）对稀疏矩阵进行操作，会浪费大量的计算资源和内存。torch.spmm()函数能高效处理稀疏矩阵和密集矩阵的乘法，它只会对非零元素进行计算，从而提高计算效率。

1
torch.spmm(mat1, mat2)
  • mat1：这是一个稀疏矩阵，其类型为torch.sparse.FloatTensor
  • mat2：这是一个密集矩阵，其类型为torch.FloatTensor

返回值：返回一个密集矩阵，类型为torch.FloatTensor，形状为(mat1.size(0), mat2.size(1))

多层GCN的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class GCN(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout=0.1):
        """
        nfeat: 各个节点输入的特征维度
        nhid: 节点第一层嵌入维度
        nclass: 输出特征维度（分类个数）
        """
        super().__init__()
        self.gc1 = GraphConvolution(nfeat, nhid)
        self.gc2 = GraphConvolution(nhid, nclass)
        self.dropout = nn.Dropout(dropout)
        
    def forward(self, x, adj):
        x = F.relu(self.gc1(x, adj))
        x = self.dropout(x)
        x = self.gc2(x, adj)
        return x

注意：adj是\(\tilde{\mathbf{D}}^{-\frac{1}{2}}\tilde{\mathbf{A}}\tilde{\mathbf{D}}^{-\frac{1}{2}}\)，可以在输入神经网络之前就处理好。

深度学习 > 理论基础
#人工智能 #神经网络 #深度学习 #图神经网络
图神经网络和GCN
https://blog.shinebook.net/2025/04/30/人工智能/理论基础/深度学习/图神经网络和GCN/
作者
X
发布于
2025年4月30日
许可协议