学习率预热和学习率衰减

学习率预热

学习率预热（Learning Rate Warmup），是一种在深度学习训练过程中调整学习率的策略。

在训练开始时，先使用一个较小的学习率，然后逐步将学习率增加到预设的正常学习率水平。这个先使用较小学习率然后逐步增加学习率到正常水平的过程就叫做学习率预热。

学习率预热的原因：

避免模型初期不稳定：在训练刚开始时，模型的参数是随机初始化的。如果此时使用较大的学习率，可能会导致模型参数更新幅度过大，使得模型在训练初期就陷入不稳定的状态，甚至无法收敛。通过学习率预热，先使用较小的学习率可以让模型在初期进行较为温和的参数调整，逐渐适应训练数据，从而提高模型训练的稳定性。
抑制梯度噪声影响：训练初期模型的预测误差较大，计算出的梯度可能包含噪声（如异常值或错误方向），大学习率会放大噪声的负面影响。预热阶段的小学习率可以降低噪声对参数更新的干扰，使模型更关注梯度中稳定的方向。
修正自适应优化器的偏差：Adam等优化器在初始阶段对梯度的一阶矩（动量）和二阶矩（梯度平方）估计不准确，导致更新方向偏差较大，预热阶段使用小学习率则可以使偏差导致模型学习方向错误的影响降低。
帮助模型更好地收敛到最优解：较小的初始学习率有助于模型在参数空间中进行更细致地搜索，避免过早陷入局部最优解。随着训练的进行，逐渐增加学习率可以让模型更快地朝着最优解的方向收敛，提高训练效率。
适应不同规模的数据集：对于大规模数据集，模型需要更多的时间来学习数据中的规律。学习率预热可以让模型在训练初期更缓慢地学习，充分利用大规模数据集中的信息，避免因为学习率过高而导致过拟合或者无法充分挖掘数据特征。

学习率衰减

学习率衰减（Learning Rate Decay）是深度学习中用于动态调整学习率的策略，是指在深度学习模型训练过程中，随着训练的进行，按照一定的策略逐渐降低学习率的方法。

一般在学习率预热之后学习率回到正常水平，之后在使用学习率衰减，逐渐降低学习率，让模型实现从“快速探索”到“精细收敛”的过度。

学习率预热之后进行学习率衰减的原因：

防止模型震荡：在训练后期，模型参数已经逐渐接近最优值。如果学习率仍然保持比较大，可能会导致参数更新时产生较大的波动，使模型在最优解附近来回震荡，无法稳定地收敛到最优解。通过学习率衰减，可以减小参数更新的步长，让模型更加平稳地收敛。
避免过拟合：较小的学习率可以使模型在训练后期对新数据的适应速度变慢，减少模型对训练数据中噪声的拟合，从而降低过拟合的风险。当学习率衰减时，模型更注重对整体数据分布的学习，而不是过度关注训练数据中的细节，有助于提高模型的泛化能力。
符合模型训练的规律：在训练初期，模型需要较大的学习率来快速探索参数空间，找到大致的最优解方向。而在训练后期，模型已经接近最优解，需要更小的学习率来进行微调，以进一步优化模型性能。学习率预热和衰减相结合，能够更好地适应模型在不同训练阶段的需求，提高训练效率和模型质量。

学习率衰减的常见方式：

固定步长衰减：每隔一定的训练步数或epochs，就按照固定的比例降低学习率。例如，每经过10个epochs，将学习率乘以0.1
指数衰减：学习率按照指数函数的形式进行衰减，公式通常为\(\mathrm{lr} = \mathrm{lr}_0\times\gamma^t\)，其中\(\mathrm{lr}_0\)是初始学习率，\(\gamma\)是衰减因子（\(0<\gamma<1\)），\(t\)是训练的步数或者epochs数。随着\(t\)的增加学习率会逐渐减小。
余弦退火衰减：(Cosine Annealing Decay)，通过余弦函数的周期性变化规律，让学习率从初始值逐渐平滑下降至最小值。在下降到最小值之后可以选择上升学习率，如此循环。 \[ \eta_t = \eta_{\min} + \frac{1}{2}(\eta_{\max}-\eta_{\min})\left(1 + \cos\left(\frac{\pi T_{\mathrm{cur}}}{T_{\max}}\right)\right) \] \(\eta_t\)是第\(t\)次迭代时的学习率，\(\eta_\min\)是学习率的最小值，\(\eta_\max\)是学习率的最大值，\(T_{\mathrm{cur}}\)是当前所处的迭代次数，\(T_\max\)是一个完整余弦退火周期内的总迭代次数。在一个周期刚开始时，余弦函数处于最大值，此时学习率\(\eta_t = \eta_\max\)，一个周期要结束时，\(T_{\mathrm{cur}}=T_\max\)，此时余弦函数处于最小值-1，\(\eta_t = \eta_\min\)。一个周期后，余弦函数又处于最大值，学习率重回最大值。

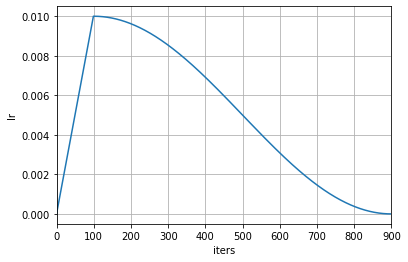
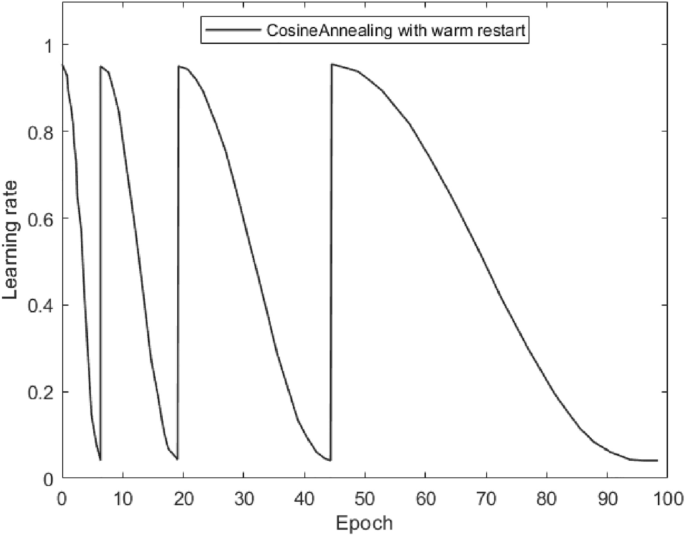
每个周期的余弦退火的周期\(T_\max\)可以不一样，越到后面可以越大，每个周期的余弦退后的\(\eta_\max\)也可以不一样，越到后面越小：

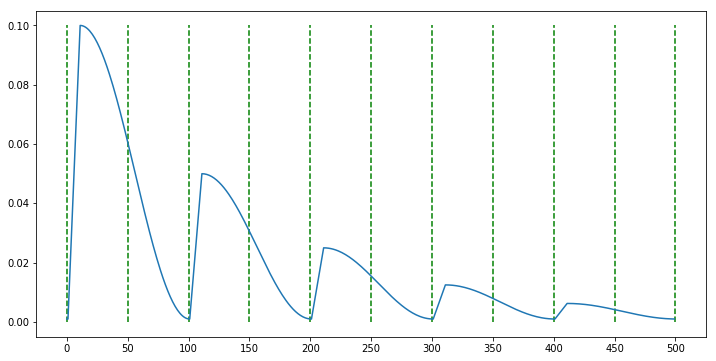
余弦退火的优点：
- 平滑过度特性：余弦退火通过余弦函数的连续型实现学习率无突变调整，相比阶梯式衰减（Step Decay）或指数衰减（Exponential Decay）的突然下降，避免了训练过程中因为学习率剧烈变化导致的震荡问题，这种平滑性使参数更新更稳定，尤其适合对噪声敏感的深度模型（如Transformer）
- 自适应阶段优化：
  - 初期大学习率：快速接近最优解区域（如余弦函数初始段的高值），加速模型早期收敛
  - 中期逐渐降低：随着训练的深入，学习率按余弦值逐渐减小，平衡收敛速度与精度
  - 后期精细调整：接近训练结束时学习率降到最低值附近，帮助模型在最优解附近微调参数
- 周期性重启机制（SGDR变体）：通过周期性重置学习率至初始值（比如每50个epoch重启一次），模拟物理退火中的“热重启”，帮助模型跳出局部最优解，探索更广的参数空间。这种机制在复杂损失曲面的任务（如GAN训练）中效果显著
- 与预热（Warmup）策略结合：在训练初期结合线性预热（逐步提升学习率），可避免参数初始阶段的剧烈震荡，与后续的余弦退火形成“先升后降”的动态调整，特别适合大规模预训练模型（如BERT、GPT）
余弦退火常用参数调整：

\(T_\max\)通常设为总训练epochs的40~60%，\(\eta_\min\)通常设为初始学习率\(\eta_\max\)的\(1/10\)，重启策略：复杂任务可以每3~5周期重启一次，并逐步延长周期长度，第\(i\)个周期的总长度计算公式为： \[ T_i = T_0\times T_{\mathrm{mult}}^{i-1} \] 则余弦退火公式为： \[ \eta_t = \eta_{\min} + \frac{1}{2}(\eta_{\max}-\eta_{\min})\left(1 + \cos\left(\frac{\pi T_{\mathrm{cur}}}{T_i}\right)\right) \] 若\(T_0=5\)且\(T_{\mathrm{mult}}=2\)，则第一个周期5个epoch，第二个周期10个epoch，第三个周期20个epoch，依此类推。

PyTorch实现

使用API实现学习率预热和衰减

import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim.lr_scheduler import CosineAnnealingLR, LinearLR, SequentialLR

# 模型与优化器初始化
model = nn.Linear(10, 2)
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 参数设置
warmup_epochs = 10
total_epochs = 100
lr_max = 0.01	# 预热后的峰值学习率
min_lr = 1e-6	# 余弦退火的最小学习率

# 定义预热调度器（线性增长）
warmup_scheduler = LinearLR(
    optimizer,	# 优化器
    start_factor=1e-5,	# 初始学习率相对于优化器中lr的缩放比例
    total_iters=warmup_epochs	# 预热的持续时长（单位：epoch或step）
)

# 定义余弦退火调度器
cosine_scheduler = CosineAnnealingLR(
    optimizer,
    T_max=total_epochs - warmup_epochs,	# 退火周期长度
    eta_min=min_lr
)

# 组合调度器
combined_scheduler = SequentialLR(
    optimizer,
    schedulers=[warmup_scheduler, cosine_scheduler],
    milestones=[warmup_epochs]	# 第10个epoch后切换为余弦退火
)

# 训练循环
for epoch in range(total_epochs):
    # 训练步骤...
    combined_scheduler.step()	# 更新学习率
    
    optimizer.step()	# 更新模型参数
    
    print(f'Epoch {epoch + 1}, LR: {optimizer.param_groups[0]['lr']}')	# 打印epoch和优化器的学习率

LinearLR调度器

线性调度器

参数：（第一个参数为设定好的优化器，下面是后面的参数介绍）

start_factor：初始学习率相对于优化器lr的缩放比例，公式：初始学习率=optimizer.lr*start_factor，典型值为1e-5（从极低学习率开始增长）
end_factor：预热结束时的学习率相对于优化器lr的缩放比例，默认为1.0（预热结束后学习率等于优化器的初始lr）
total_iters：预热持续的时长（单位epoch或step），在这个期间学习率由初始学习率到结束时学习率线性增长，典型值为总训练epoch的5~10%

比如：

warmup_scheduler = LinearLR(
    optimizer,
    start_factor=1e-5,
    total_iters=5
)

CosineAnnealingLR调度器

余弦退火调度器

参数：

T_max：余弦周期长度（单位：epoch或step），如果整个训练中只有一个周期，那么就设为总epochs减去预热的epochs：T_max=total_epochs - warmup_epochs
eta_min：学习率的最小下限值，典型值：1e-6~1e-4，若设为0，可能导致训练后期停滞

比如：

cosine_scheduler = CosineAnnealingLR(
    optimizer,
    T_max=50-5,
    eta_min=1e-5
)

CosineAnnealingWarmRestarts调度器

周期性重启的余弦退火调度器

参数：

T_max：余弦周期长度（单位：epoch或step），如果整个训练中只有一个周期，那么就设为总epochs减去预热的epochs：T_max=total_epochs - warmup_epochs
eta_min：学习率的最小下限值，典型值：1e-6~1e-4，若设为0，可能导致训练后期停滞
T_0：初始的周期长度（单位：epoch或step）
T_mult：周期长度的增长倍数

比如：

cosine_restart_scheduler = CosineAnnealingWarmRestarts(
    optimizer,
    T_max=100,
    eta_min=1e-5,
    T_0=5,
    T_mult=2
)

ConsineAnnealingWarmRestarts调度器会在一个周期结束后瞬间将学习率变为最大值，进入下一个周期。

一般来说，该调度器无需搭配其他调度器使用

StepLR调度器

每隔固定的训练轮数（step_size），学习率就会乘以一个固定的衰减因子（gamma），公式为 \[ \eta_t = \eta_{t-1}\times\gamma \] 当\(t\ \ \mathrm{mod}\ \ \mathrm{step\_size} = 0\)时，更新学习率

参数：

step_size
gamma

比如：

from torch.optim.lr_scheduler import StepLR

# ...
scheduler = StepLR(
    optimizer,
    step_size=30,
    gamma=0.1
)

MultiStepLR调度器

在预先指定的训练轮数（milestones）处，学习率乘以一个固定的衰减因子（gamma）。与StepLR不同的是，它不是按照固定间隔衰减，而是在特定的轮数衰减

参数：

milestones：列表，指定衰减的epoch或step处
gamma

比如：

from torch.optim.lr_scheduler import MultiStepLR

# ...
scheduler = MultiStepLR(
    optimizer,
    milestones=[30, 80],
    gamma=0.1
)

ExponentialLR调度器

学习率按照指数函数的形式进行衰减，每一轮学习率都会乘以一个固定的衰减因子（gamma），公式为 \[ \eta_t = \eta_0\times\gamma^t \] 其中\(\eta_0\)是初始学习率，\(t\)是训练轮数

参数：

gamma

比如：

from torch.optim.lr_scheduler import ExponentialLR

# ...
scheduler = ExponentialLR(
    optimizer,
    gamma=0.95
)

ReduceLROnPlateau调度器

当某个指标（如验证集损失）在一定轮数（patience）内没有改善时，学习率会乘以一个衰减因子（factor），适用于根据验证集性能动态调整学习率的情况，能有效避免模型过早陷入局部最优，提高模型的泛化能力。

参数：

mode：(str)，模式，可以是min或max。如果是min，当监控的指标不再下降时，学习率更新；如果是max，当监控的指标不再上升时，学习率更新。默认值是min
factor：(float)，学习率衰减因子，每次调整学习率时，学习率会乘以factor
patience：(int)，容忍度，即指标在多少个连续的训练周期内没有改善后，才会降低学习率。默认值是10
verbose：(bool)，如果为True，则在学习率调整时会打印出相关信息，如当前学习率和调整后的学习率等，默认值是False
threshold：(float)，衡量指标是否有显著变化的阈值，只有当指标的变化超过这个阈值时，才会认为指标有改善，默认值是1e-4
threshold_mode (str)：与threshold配合使用，指定如何比较指标的变化与阈值。可以是rel（相对变化）或abs（绝对变化）。如果是rel，则指标的相对变化超过threshold时认为有改善；如果是abs，则指标的绝对变化超过threshold时认为有改善。默认值是rel。
cooldown (int)：学习率降低后，需要经过多少个周期的冷却时间，才会再次开始监控指标以决定是否继续降低学习率。默认值是0。
min_lr (float 或 list)：学习率的下限。可以是一个浮点数，表示所有参数组的学习率下限；也可以是一个列表，为每个参数组指定不同的学习率下限。默认值是0。
eps (float)：学习率衰减的最小值。当学习率的变化小于eps时，不再进行衰减。默认值是1e-8。

比如：

from torch.optim.lr_scheduler import ReduceLROnPlateau

scheduler = ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=5, verbose=True)

for epoch in range(100):
    # 训练步骤
    optimizer.zero_grad()
    output = model(torch.randn(100, 10))
    loss = nn.MSELoss()(output, torch.ones(100, 1))
    loss.backward()
    optimizer.step()

    # 假设val_loss是验证集的损失
    val_loss = torch.rand(1).item()
    scheduler.step(val_loss)

ConstantLR调度器

让学习率在训练期间保持恒定

参数：

factor：学习率的缩放因子。在 total_iters 次迭代内，学习率会是初始学习率乘以 factor；超过 total_iters 后，学习率恢复到初始值。默认值是 0.3333333333333333。相当于学习率预热。
total_iters：指定学习率保持为初始学习率乘以 factor 的迭代次数。默认值是 5。
last_epoch：上一轮的轮数，默认是 -1，表示从初始学习率开始。如果要暂停训练后接着恢复，可设置这个参数来指定恢复训练时的起始轮数。

比如：

1	`scheduler = ConstantLR(optimizer, factor=0.3333333333333333, total_iters=5, last_epoch=-1)`

组合调度器（SequentialLR）

参数：

schedulers：按顺序执行的调度器列表
milestones：定义何时切换到下一个调度器，列表，长度必须为schedulers列表长度减一，比如[10, 30]，表示第0~10epoch使用第一个调度器，第11~30epoch使用第二个调度器，第31+epoch使用第三个调度器

比如：

scheduler = SequentialLR(
    optimizer,
    schedulers=[warmup, cosine, constant],
    milestones=[10, 100]
)

自定义调度器

继承基类_LRScheduler：

from torch.optim.lr_scheduler import _LRScheduler

class CustomScheduler(_LRScheduler):
    def __init__(self, optimizer, param1, params2, last_epoch=-1):
        # last_epoch: 当前训练步数，默认值为`-1`，表示未开始训练
        self.param1 = param1
        self.param2 = param2
        super().__init__(optimizer, last_epoch)	# 调用父类_LRScheduler的构造函数，初始化优化器和当前训练步数
        # 调用父类构造函数后，optimizer会存储到self.optimizer，last_epoch会存储到self.last_epoch

向父类构造函数传递optimizer和last_epoch，因为父类需要直接操作优化器的学习率，例如，若scheduler = CustomScheduler(optimizer, 1, 2)，在scheduler.step()中，父类会调用self.optimizer.param_groups[0]['lr'] = new_lr，并且，父类会校验优化器的合法性，并保存起初始学习率到self.base_lrs

若last_epoch=-1，父类将其初始化为-1（self.last_epoch=-1），表示训练未开始，首次调用scheduler.step()时，self.last_epoch会自增为0

定义get_lr()函数，用于返回当前学习率：

# 定义一个线性调度器（LinearLR）
class CustomLinearLR(_LRScheduler):
    def __init__(self, optimizer, start_factor, total_iters, end_factor=1.0, last_epoch=-1):
        self.start_factor = start_factor
        self.end_factor = end_factor
        self.total_iters = total_iters
        super().__init__(optimizer, last_epoch)
        
    def get_lr(self):
        step = self.last_epoch + 1
        
        # 限制step不超过self.total_iters
        step = min(step, self.total_iters)
        
        return [base_lr * (self.start_factor + (self.end_factor - self.start_factor)/self.total_iters*step) for base_lr in self.base_lrs]

get_lr()函数用于返回当前学习率，返回的是一个列表，列表中的每个元素代表优化器中不同参数组（Parameter Group）的当前学习率（一个优化器可以设置不同的参数组提供不同的学习率，这在之前优化器的部分有写过），不同参数组的初始学习率存储在self.base_lrs中。

在调用scheduler.step()时，self.last_epoch会自增1，然后会调用get_lr()函数，得到当前学习率，将当前学习率应用到优化器中。

深度学习 > 理论基础

#人工智能 #神经网络 #深度学习

学习率预热和学习率衰减

https://blog.shinebook.net/2025/04/25/人工智能/理论基础/深度学习/学习率预热和学习率衰减/

作者

发布于

2025年4月25日

许可协议

梯度裁剪上一篇

Transformer 下一篇