多头自注意力机制

自注意力机制

在之前的机器翻译中，使用注意力机制的Seq2Seq模型，\(\mathbf{K}\)、\(\mathbf{V}\)是编码器中所有时间步的最后一个时间步的隐藏状态，\(\mathbf{Q}\)是解码器中当前时间步隐藏状态输入（即上一个时间步的隐藏状态输出）\(\mathbf{H}_{t-1}\)，以此来决定当前时间步的输出更应该关注编码器哪些信息。

与这种注意力机制不同的是，自注意力机制（Self-attention）的\(\mathbf{K}\)、\(\mathbf{V}\)、\(\mathbf{Q}\)均为对输入序列\(\mathbf{X}\)的线性变换，其中\(\mathbf{X}\in\mathbb{R}^{m\times d}\)，\(m\)表示一共有\(m\)个时间步，\(d\)表示一个时间步的输入是维度为\(d\)的向量\(\mathbf{x}_i\)（\(\mathbf{X}\)仅代表一个样本的数据） \[ \begin{aligned} &\mathbf{K} = \mathbf{X}\cdot\mathbf{W}_k\in\mathbb{R}^{m\times d}\\ &\mathbf{Q} = \mathbf{X}\cdot\mathbf{W}_q\in\mathbb{R}^{m\times d}\\ &\mathbf{V} = \mathbf{X}\cdot\mathbf{W}_v\in\mathbf{R}^{m\times d} \end{aligned} \] 其中，\(\mathbf{W}_k, \mathbf{W}_q, \mathbf{W}_v\in\mathbb{R}^{d\times d}\)，

使用缩放点积注意力： \[ f(\mathbf{Q}) = \mathrm{softmax}\left(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d}}\right)\mathbf{V}\in\mathbb{R}^{m\times d} \] 其中， \[ \begin{aligned} \frac{\mathbf{Q}\mathbf{K}^T}{\sqrt{d}} &= \frac{1}{\sqrt{d}}\left[ \begin{matrix} \mathbf{q}_1\\ \mathbf{q}_2\\ \vdots\\ \mathbf{q}_m \end{matrix} \right] \left[ \begin{matrix} \mathbf{k}_1^\top&\mathbf{k}_2^\top&\cdots&\mathbf{k}_m^\top \end{matrix} \right]\\ \\ &= \left[ \begin{matrix} \frac{\mathbf{q}_1\mathbf{k}_1^\top}{\sqrt{d}}&\frac{\mathbf{q}_1\mathbf{k}_2^\top}{\sqrt{d}}&\cdots&\frac{\mathbf{q}_1\mathbf{k}_m^\top}{\sqrt{d}}\\ \frac{\mathbf{q}_2\mathbf{k}_1^\top}{\sqrt{d}}&\frac{\mathbf{q}_2\mathbf{k}_2^\top}{\sqrt{d}}&\cdots&\frac{\mathbf{q}_2\mathbf{k}_m^\top}{\sqrt{d}}\\ \vdots&\vdots& &\vdots\\ \frac{\mathbf{q}_m\mathbf{k}_1^\top}{\sqrt{d}}&\frac{\mathbf{q}_m\mathbf{k}_2^\top}{\sqrt{d}}&\cdots&\frac{\mathbf{q}_m\mathbf{k}_m^\top}{\sqrt{d}} \end{matrix} \right]\\ \\ &= \left[ \begin{matrix} a(\mathbf{q}_1, \mathbf{k}_1)&a(\mathbf{q}_1, \mathbf{k}_2)&\cdots&a(\mathbf{q}_1, \mathbf{k}_m)\\ a(\mathbf{q}_2, \mathbf{k}_1)&a(\mathbf{q}_2, \mathbf{k}_2)&\cdots&a(\mathbf{q}_2, \mathbf{k}_m)\\ \vdots&\vdots& &\vdots\\ a(\mathbf{q}_m, \mathbf{k}_1)&a(\mathbf{q}_m, \mathbf{k}_2)&\cdots&a(\mathbf{q}_m, \mathbf{k}_m) \end{matrix} \right] \in\mathbb{R}^{m\times m} \end{aligned} \]

因为 \[ \alpha(\mathbf{q}_i, \mathbf{k}_j) = \mathrm{softmax}(a(\mathbf{q}_i, \mathbf{k}_j)) = \frac{a(\mathbf{q}_i, \mathbf{k}_j)}{\sum_{s=1}^m a(\mathbf{q}_i, \mathbf{k}_s)}\in\mathbb{R} \] 则 \[ \begin{aligned} f(\mathbf{Q}) &= \mathrm{softmax}\left(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d}}\right)\mathbf{V}\\ \\ &= \left[ \begin{matrix} \alpha(\mathbf{q}_1, \mathbf{k}_1)&\alpha(\mathbf{q}_1, \mathbf{k}_2)&\cdots&\alpha(\mathbf{q}_1, \mathbf{k}_m)\\ \alpha(\mathbf{q}_2, \mathbf{k}_1)&\alpha(\mathbf{q}_2, \mathbf{k}_2)&\cdots&\alpha(\mathbf{q}_2, \mathbf{k}_m)\\ \vdots&\vdots& &\vdots\\ \alpha(\mathbf{q}_m, \mathbf{k}_1)&\alpha(\mathbf{q}_m, \mathbf{k}_2)&\cdots&\alpha(\mathbf{q}_m, \mathbf{k}_m) \end{matrix} \right]\cdot\left[ \begin{matrix} \mathbf{v}_1\\ \mathbf{v}_2\\ \vdots\\ \mathbf{v}_m \end{matrix} \right]\\ \\ &= \left[ \begin{matrix} \alpha(\mathbf{q}_1, \mathbf{k}_1)\mathbf{v}_1 + \alpha(\mathbf{q}_1, \mathbf{k}_2)\mathbf{v}_2 + \cdots + \alpha(\mathbf{q}_1, \mathbf{k}_m)\mathbf{v}_m\\ \alpha(\mathbf{q}_2, \mathbf{k}_1)\mathbf{v}_1 + \alpha(\mathbf{q}_2, \mathbf{k}_2)\mathbf{v}_2 + \cdots + \alpha(\mathbf{q}_2, \mathbf{k}_m)\mathbf{v}_m\\ \vdots\\ \alpha(\mathbf{q}_m, \mathbf{k}_1)\mathbf{v}_1 + \alpha(\mathbf{q}_m, \mathbf{k}_2)\mathbf{v}_2 + \cdots + \alpha(\mathbf{q}_m, \mathbf{k}_m)\mathbf{v}_m \end{matrix} \right]\\ \\ &= \left[ \begin{matrix} f(\mathbf{q}_1)\\ f(\mathbf{q}_2)\\ \vdots\\ f(\mathbf{q}_m) \end{matrix} \right] \end{aligned} \]

\[ f(\mathbf{q}_i) = \sum_{j=1}^m \alpha(\mathbf{q}_i, \mathbf{k}_j)\mathbf{v}_j\in\mathbb{R}^{d} \]

\(f(\mathbf{q}_i)\)可以认为是信息\(\mathbf{v}_i\)的加权平均，而\(\alpha(\mathbf{q}_i, \mathbf{k}_j)\)则衡量了\(\mathbf{v}_j\)对于\(f(\mathbf{q}_i)\)的重要性，因此，可以认为\(\alpha(\mathbf{q}_i, \mathbf{k}_j)\)代表了\(\mathbf{q}_i\)与\(\mathbf{v}_j\)的相关性（越相关则越重要），\(\mathbf{k}_j\)则代表了\(v_j\)的特征

由于自注意力机制的\(\mathbf{K}\)、\(\mathbf{Q}\)、\(\mathbf{V}\)均为\(\mathbf{X}\)的线性变换，因此我们可以其就代表\(\mathbf{X}\)的信息，那么，\(\alpha(\mathbf{q}_i, \mathbf{k}_i)\)就代表了\(\mathbf{x}_i\)与\(\mathbf{x}_j\)的相关性，以概率的形式表示，概率值越大则越相关，那么，\(\mathrm{softmax}\left(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d}}\right)\)的第\(i\)行第\(j\)列元素就代表了\(\mathbf{x}_i\)与\(\mathbf{x}_j\)的相关性

对于自注意力机制，输入数据\(\mathbf{X}\)与输出数据\(f(\mathbf{Q})\)维度均为\(\mathbb{R}^{m\times d}\)

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import torch
import torch.nn as nn

class SelfAttention(nn.Module):
    def __init__(self, x_dim):
        self.x_dim = x_dim
        self.query = nn.Linear(x_dim, x_dim)	# 保留偏置可以增强模型非线性拟合能力，删去偏置可以简化模型
        self.key = nn.Linear(x_dim, x_dim)
        self.value = nn.Linear(x_dim, x_dim)
        
    def forward(self, x, mask=None):
        # 生成Q、K、V
        Q = self.query(x)
        K = self.key(x)
        V = self.value(x)
        
        scores = torch.matmul(Q, K.transpose(-2, -1)) / torch.sqrt(torch.tensor(self.x_dim))
        
        if mask is not None:
            scores = scores.masked_fill(mask==0, -1e9)
            
        attn_weights = torch.softmax(scores, dim=-1)
        out = torch.matmul(attn_weights, V)
        return out

下面探讨一下\(\mathbf{K}\)、\(\mathbf{Q}\)、\(\mathbf{V}\)每个元素代表的具体内容： \[ \begin{aligned} \mathbf{K} &= \mathbf{X}\mathbf{W}_k\\ &= \left[ \begin{matrix} \mathbf{x}_1\\ \mathbf{x}_2\\ \vdots\\ \mathbf{x}_m \end{matrix} \right]\cdot\left[ \begin{matrix} \mathbf{w}_1&\mathbf{w}_2&\cdots&\mathbf{w}_d \end{matrix} \right]\\ &= \left[ \begin{matrix} \mathbf{x}_1\mathbf{w}_1&\mathbf{x}_1\mathbf{w}_2&\cdots&\mathbf{x}_1\mathbf{w}_d\\ \mathbf{x}_2\mathbf{w}_1&\mathbf{x}_2\mathbf{w}_2&\cdots&\mathbf{x}_2\mathbf{w}_d\\ \vdots&\vdots& &\vdots\\ \mathbf{x}_m\mathbf{w}_1&\mathbf{x}_m\mathbf{w}_2&\cdots&\mathbf{x}_m\mathbf{w}_d \end{matrix} \right]\\ &= \left[ \begin{matrix} \mathbf{k}_1\\ \mathbf{k}_2\\ \vdots\\ \mathbf{k}_m \end{matrix} \right] \end{aligned} \] \(\mathbf{x}_t\)表示第\(t\)个时间步的输入向量，因为： \[ \mathbf{k}_t = [\begin{matrix}\mathbf{x}_t\mathbf{w}_1&\mathbf{x}_t\mathbf{w}_2&\cdots&\mathbf{x}_t\mathbf{w}_d\end{matrix}] \] 因此，\(\mathbf{k}_t\)表示第\(t\)个时间步\(\mathbf{x}_t\)的线性组合： \[ \mathbf{k}_t = \mathbf{x}_t\mathbf{W}_k \] 则，\(\mathbf{K}\)的每行为样本的一个时间步的线性组合，同理得到的\(\mathbf{Q}\)、\(\mathbf{V}\)第\(t\)行代表样本第\(t\)个时间步的线性组合。

位置编码

在处理时序序列时（比如词元序列），循环神经网络是逐个地重复处理词元的，而自注意力机制则为并行计算而放弃了顺序操作。而位置编码（Positional Encoding）是一种在序列数据中为模型提供元素位置信息的技术，弥补自注意力机制模型因并行而无法感知序列顺序的缺陷。

位置编码通过向序列中的每个元素（如词向量）添加一个位置相关的向量，使模型能够感知元素在序列中的绝对或相对位置。

使用固定公式生成位置向量，假设输入表示\(\mathbf{X}\in\mathbb{R}^{m\times d}\)，表示一个序列中\(m\)个时间步，每个时间步为一个\(d\)维度的向量。位置编码使用相同形状的位置嵌入矩阵\(\mathbf{P}\in\mathbb{R}^{m\times d}\)，其中\(\mathbf{P}\)的第\(i\)行第\(2j\)列和\(2j+1\)列上的元素为（\(i\)、\(j\)均从0开始）： \[ \begin{aligned} &P_{i, 2j} = \sin\left(\frac{i}{10000^{2j/d}}\right)\\ \\ &P_{i,2j+1} = \cos\left(\frac{i}{10000^{2j/d}}\right) \end{aligned} \] \(\mathbf{X}\)的每行代表一个时间步的向量，每列代表不同时间步的元素向量的同一个位置。当列不变时，两个三角函数的周期不变，随着行数的增加三角函数进行周期性的变化。当行不变时，随着列数的增加，两个三角函数的周期逐渐增大。

这与数字在个位、十位、百位上的周期不同相似，比如对于二进制数据：

1
2
3
4
5
6
7
8
0的二进制是：000
1的二进制是：001
2的二进制是：010
3的二进制是：011
4的二进制是：100
5的二进制是：101
6的二进制是：110
7的二进制是：111

该现象周期在一定程度上可以解释位置编码不同列上周期改变可以学习数据的绝对位置信息。

以热力图的形式体现不同行不同列位置编码矩阵\(\mathbf{P}\)的数据大小：

由于对于不同的行，\(\mathbf{P}_i\)（行向量）的值不同，对于不同的列，\(\mathbf{P}_{,j}\)（列向量）的值也不同，让模型学会位置编码的这些内容，就可以识别\(\mathbf{X}_{i,j}\)的绝对位置信息。

除了捕获绝对位置信息外，上述的位置编码还允许模型学习得到输入序列中的相对位置信息。这是因为对于任意确定的位置偏移\(\delta\)，位置\(i+\delta\)处的位置编码可以线性投影位置\(i\)处的位置编码来表示。

令\(\omega_j = 1/10000^{2j/d}\)，对于任何确定的位置偏移\(\delta\)，位置编码矩阵\(\mathbf{P}\)中的任何一对\((p_{i,2j}, p_{i,2j+1})\)都可以线性投影到\((p_{i+\delta,2j},p_{i+\delta,2j+1})\)： \[ \begin{split}\begin{aligned} &\left[ \begin{matrix} \cos(\delta\omega_j)&\sin(\delta\omega_j)\\ -\sin(\delta\omega_j)&\cos(\delta\omega_j) \end{matrix} \right]\left[ \begin{matrix} p_{i,2j}\\ p_{i,2j+1} \end{matrix} \right]\\ \\ =& \left[ \begin{matrix} \cos(\delta\omega_j)\sin(i\omega_j) +\sin(\delta\omega_j)\cos(i\omega_j)\\ -\sin(\delta\omega_j)\sin(i\omega_j) + \cos(\delta\omega_j)\cos(i\omega_j) \end{matrix} \right]\\ \\ =& \left[ \begin{matrix} \sin((i+\delta)\omega_j)\\ \cos((i+\delta)\omega_j) \end{matrix} \right] \\ \\ =& \left[ \begin{matrix} p_{i+\delta, 2j}\\ p_{i+\delta, 2j+1} \end{matrix} \right] \end{aligned}\end{split} \] \(2\times 2\)的投影矩阵不依赖任何位置的索引\(i\)，令 \[ \mathbf{R}(\delta) = \left[ \begin{matrix} \cos(\delta\omega_j)&\sin(\delta\omega_j)\\ -\sin(\delta\omega_j)&\cos(\delta\omega_j) \end{matrix} \right] \] 线性变换矩阵\(\mathbf{R}(\delta)\)仅与\(\delta\)有关，与\(i\)无关，这种设计使得相对位置偏差\(\delta\)的数学表达独立于绝对位置\(i\)，模型无需记忆具体位置，只需要学习\(\delta\)的变换模式即可推断相对距离

多头注意力机制

之前的使用注意力机制的Seq2Seq模型中，我们仅使用了一个注意力机制，我们也可以同时使用多个注意力机制，然后将这些注意力连接，通过一个线性层投影到原本一个注意力机制的维度，由于每个注意力机制都有可学习的参数，因此不同的注意力机制可以学习到不同的内容。多头注意力机制（Multi-head Attention）中的多头，实际上指的就是多个注意力机制，而使用多少个注意力机制是一个可以人为调控的超参数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 使用两个注意力机制的Seq2Seq
class Decoder(nn.Module):
    def __init__(self, vocab_size, embed_size, dec_hidden_size, enc_hidden_size, attention1, attention2):
        super().__init__()
        self.attention1 = attention1
        self.attention2 = attention2
        self.trg_vocab_size = vocab_size
        
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(embed_size + enc_hidden_size*2, dec_hidden_size, batch_first=True)
        self.fc_attn = nn.Linear(enc_hidden_size*4, enc_hidden_size*2)
        self.fc = nn.Linear(dec_hidden_size + enc_hidden_size*2 + embed_size, vocab_size)
        
    def forward(self, input, hidden, encoder_outputs):
        input = input.unsqueeze(1)
        embedded = self.embedding(input)
        
        context1, _ = self.attention1(
            keys=encoder_outputs,
            values=encoder_outputs,
            queries=hidden
        )# [batch_size, encoder_hidden_size*2]
        
        context2, _ = self.attention2(
            keys=encoder_outputs,
            values=encoder_outputs,
            queries=hidden
        )# [batch_size, encoder_hidden_size*2]
        context = torch.cat((context1, context2), dim=1) # [batch_size, encoder_hidden_size*4]
        context = self.fc_attn(context) # [batch_size, encoder_hidden_size*2]
        
        # ......

多头自注意力机制

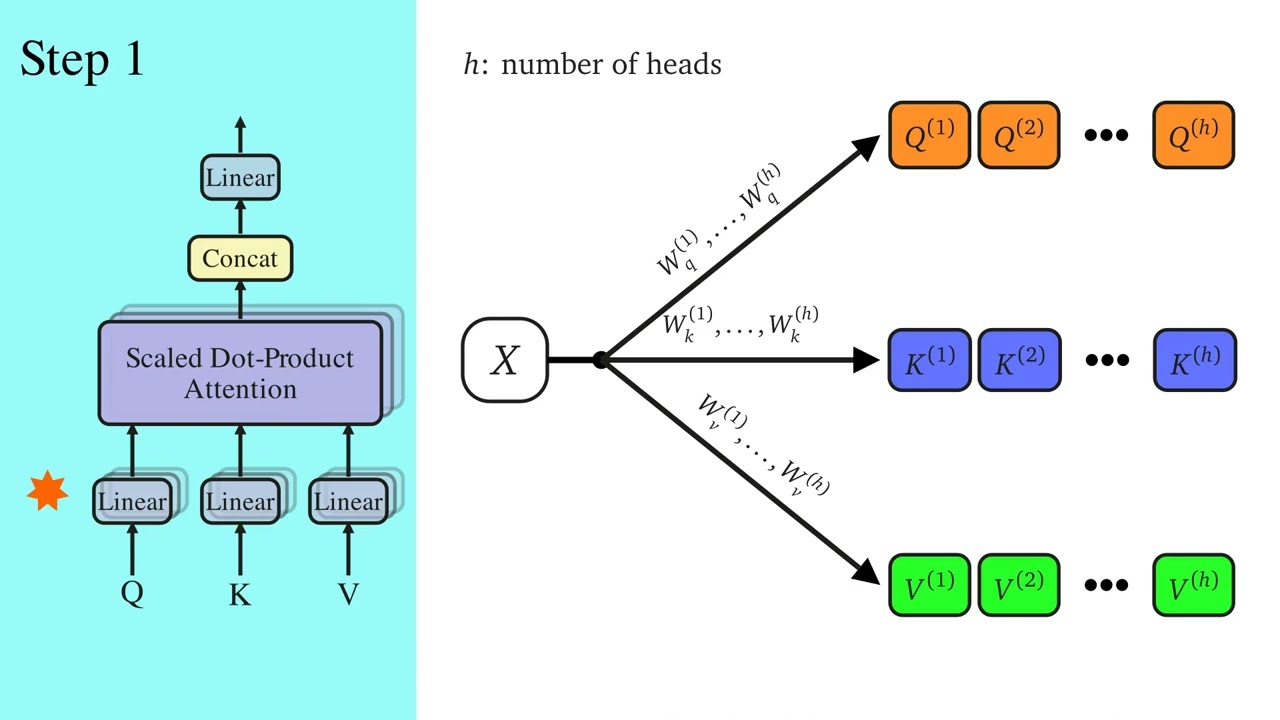
对一个样本的输入序列\(\mathbf{X}\in\mathbb{R}^{m\times d}\)，可以使用多个自注意力机制生成多个\((\mathbf{K}, \mathbf{Q}, \mathbf{V})\)，得到多个注意力机制的结果\(f(\mathbf{K}, \mathbf{Q}, \mathbf{V})\)，在Transformer的多头自注意力机制中，输入样本\(\mathbf{X}\)经过线性投影生成\(n\)个\((\mathbf{K}, \mathbf{Q}, \mathbf{V})\)，每个注意力仅保留\(\frac{d}{n}\)的维度（一共有\(n\)个头），对每个\((\mathbf{K}_i, \mathbf{Q}_i, \mathbf{V}_i)\)： \[ \mathbf{K}_i, \mathbf{Q}_i, \mathbf{V}_i\in\mathbb{R}^{m\times \frac{d}{n}} \] 令\(d_h = \frac{d}{n}\)，则 \[ \mathrm{head}_i = \mathrm{Attention}(\mathbf{Q}_i, \mathbf{K}_i, \mathbf{V}_i) = \mathrm{softmax}\left(\frac{\mathbf{Q}_i\mathbf{K}_i^\top}{\sqrt{d_h}}\right)\mathbf{V}_i\in\mathbb{R}^{m\times \frac{d}{n}} \] 然后拼接所有注意力（头）并通过线性层整合映射： \[ \begin{aligned} &\mathbf{Y} = \mathrm{Concat}(\mathrm{head}_1, \mathrm{head_2}, \cdots, \mathrm{head}_n) \in\mathbb{R}^{m\times d}\\ &\mathbf{Z} = \mathbf{Y}\mathbf{W}_o\in\mathbb{R}^{m\times d} \end{aligned} \] 其中，\(\mathbf{W}_o\in\mathbb{R}^{d\times d}\)为输出投影矩阵，保持输出维度与输入维度一致。

但这样分别生成\(n\)个\((\mathbf{K}, \mathbf{Q}, \mathbf{V})\)太过麻烦，在具体的代码实现中，先通过一个线性映射统一生成维度为\(\mathbb{R}^{m\times d}\)的\(\mathbf{Q}\)、\(\mathbf{K}\)、\(\mathbf{V}\)：

1
K = self.k_proj(x)

\[ \begin{aligned} \mathbf{K} &= \mathbf{X}\mathbf{W}_k\\ &= \left[ \begin{matrix} \mathbf{k}_1\\ \mathbf{k}_2\\ \vdots\\ \mathbf{k}_m \end{matrix} \right]\\ &= \left[ \begin{matrix} k_{11}&k_{12}&\cdots&k_{1d}\\ k_{21}&k_{22}&\cdots&k_{2d}\\ \vdots&\vdots& &\vdots\\ k_{m1}&k_{m2}&\cdots&k_{md} \end{matrix} \right] \end{aligned} \] 其中 \[ \mathbf{k}_i = \left[ \begin{matrix} k_{i1}&k_{i2}&\cdots&k_{id} \end{matrix} \right] \] 是样本第\(i\)个时间步的线性组合， \[ k_{ij} = x_{i1}w_{1j} + x_{i2}w_{2j} + \cdots + x_{id}w_{dj} \] 拆分：

1
K = K.view(batch_size, seq_len, num_heads, head_dim) # seq_len=m, num_heads=n, head_dim=d/n

由于是对每个样本进行处理，不会跨样本变换维度，下面只看一个样本： \[ \begin{aligned} \mathbf{K}' &= \left[ \begin{matrix} \left[ \begin{matrix} k_{11}&k_{12}&\cdots&k_{1,d/n}\\ k_{1,d/n\ +1}&k_{1,d/n\ +2}&\cdots&k_{1,2d/n}\\ \vdots&\vdots& &\vdots\\ k_{1,(n-1)d/n\ +1}&k_{1,(n-1)d/n\ + 2}&\cdots&k_{1,d} \end{matrix} \right]\\ \\ \left[ \begin{matrix} k_{21}&k_{22}&\cdots&k_{2,d/n}\\ k_{2,d/n\ +1}&k_{2,d/n\ +2}&\cdots&k_{2,2d/n}\\ \vdots&\vdots& &\vdots\\ k_{2,(n-1)d/n\ +1}&k_{2,(n-1)d/n\ + 2}&\cdots&k_{2,d} \end{matrix} \right]\\ \\ \vdots\\ \\ \left[ \begin{matrix} k_{m1}&k_{m2}&\cdots&k_{m,d/n}\\ k_{m,d/n\ +1}&k_{m,d/n\ +2}&\cdots&k_{m,2d/n}\\ \vdots&\vdots& &\vdots\\ k_{m,(n-1)d/n\ +1}&k_{m,(n-1)d/n\ + 2}&\cdots&k_{m,d} \end{matrix} \right] \end{matrix} \right]\in\mathbb{R}^{m\times n\times \frac{d}{n}} \end{aligned} \] 然后重组：

1
K = K.transpose(1, 2) # 未变换之前维度为[batch_size, seq_len, num_heads, head_dim]，变换后为[batch_size, num_heads, seq_len, head_dim]

\[ \begin{aligned} \mathbf{K}'' = \left[ \begin{matrix} \left[ \begin{matrix} k_{11}&k_{12}&\cdots&k_{1,d/n}\\ k_{21}&k_{22}&\cdots&k_{2,d/n}\\ \vdots&\vdots& &\vdots\\ k_{m1}&k_{m2}&\cdots&k_{m,d/n} \end{matrix} \right]\\ \\ \left[ \begin{matrix} k_{1,d/n\ +1}&k_{1,d/n\ +2}&\cdots&k_{1,2d/n}\\ k_{2,d/n\ +1}&k_{2,d/n\ +2}&\cdots&k_{2,2d/n}\\ \vdots&\vdots& &\vdots\\ k_{m,d/n\ +1}&k_{m,d/n\ +2}&\cdots&k_{m,2d/n}\\ \end{matrix} \right]\\ \\ \vdots\\ \\ \left[ \begin{matrix} k_{1,(n-1)d/n\ +1}&k_{1,(n-1)d/n\ + 2}&\cdots&k_{1,d}\\ k_{2,(n-1)d/n\ +1}&k_{2,(n-1)d/n\ + 2}&\cdots&k_{2,d}\\ \vdots&\vdots& &\vdots\\ k_{m,(n-1)d/n\ +1}&k_{m,(n-1)d/n\ + 2}&\cdots&k_{m,d} \end{matrix} \right] \end{matrix} \right] \end{aligned}\in\mathbb{R}^{n\times m\times \frac{d}{n}} \]

对于\(\mathbf{K}''\)中的任意一个矩阵，比如： \[ \left[ \begin{matrix} k_{11}&k_{12}&\cdots&k_{1,d/n}\\ k_{21}&k_{22}&\cdots&k_{2,d/n}\\ \vdots&\vdots& &\vdots\\ k_{m1}&k_{m2}&\cdots&k_{m,d/n} \end{matrix} \right] \] 其第一行为原本\(\mathbf{k}_1\)的部分元素，而\(\mathbf{k}_1\)是一个样本第一个时间步的线性组合，那么\(\mathbf{k''_{1,1}}\)（即\(\mathbf{K}''\)的第一个矩阵\(\mathbf{k''_1}\)的第一行）也是一个样本第一个时间步的线性组合，只是线性方程的数量为\(\mathbf{k}_1\)线性组合线性方程数量的\(1/n\)，那么，\(\mathbf{k}''_1\)的第\(i\)行就代表了一个样本第\(i\)个时间步的线性组合，因此，\(\mathbf{k}''_i\)就是样本\(\mathbf{X}\)经过线性映射的结果，是\(n\)个注意力机制中第\(i\)个注意力机制的key，对\(\mathbf{Q}\)、\(\mathbf{V}\)的推导同理，这种先整体线性变换再拆分重组的方式与先生成\(n\)个key、value、query分别线性映射的结果相同。先整体再拆分重组的方法的优点是可以并行化进行，在GPU上可以加快模型运行速度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import torch
import torch.nn as nn
import math

class MultiHeadSelfAttention(nn.Module):
    def __init__(self, embed_dim, num_heads, dropout=0.1):
        super().__init__()
        assert embed_dim % num_heads == 0, "嵌入维度必须能被头的数量整除"
        
        self.embed_dim = embed_dim
        self.num_heads = num_heads
        self.head_dim = embed_dim // num_heads
        
        # 定义Q/K/V的线性投影层(生成Q/K/V)
        self.q_proj = nn.Linear(embed_dim, embed_dim)
        self.k_proj = nn.Linear(embed_dim, embed_dim)
        self.v_proj = nn.Linear(embed_dim, embed_dim)
        
        # 输出层和dropout
        self.out_proj = nn.Linear(embed_dim, embed_dim)
        self.dropout = nn.Dropout(dropout)
        
        # 缩放因子
        self.scale = 1.0 / math.sqrt(self.head_dim)
        
        
    def forward(self, x):
        batch_size, seq_len, _ = x.shape
        
        # 线性投影生成Q/K/V
        Q = self.q_proj(x)	# [batch_size, seq_len, embed_dim]
        K = self.k_proj(x)	# [batch_size, seq_len, embed_dim]
        V = self.v_proj(x)	# [batch_size, seq_len, embed_dim]
        
        # 分头处理（并行化核心）
        Q = Q.view(batch_size, seq_len, self.num_heads, self.head_dim).transpose(1, 2)	# [batch_size, num_heads, seq_len, head_dim]
        K = K.view(batch_size, seq_len, self.num_heads, self.head_dim).transpose(1, 2)
        V = V.view(batch_size, seq_len, self.num_heads, self.head_dim).transpose(1, 2)
        
        # 计算缩放点积注意力
        attn_score = torch.matmul(Q, K.transpose(-2, -1)) * self.scale	# [batch_size, num_heads, seq_len, seq_len]
        # softmax归一化
        attn_weights = torch.softmax(attn_score, dim=-1)
        attn_weights = self.dropout(attn_weights)
        
        # 加权求和与拼接
        context = torch.matmul(attn_weights, V)	# [batch_size, num_heads, seq_len, head_dim]
        context = context.transpose(1, 2).contiguous().view(batch_size, seq_len, -1)
        
        # 投影输出
        output = self.out_proj(context)
        return output, attn_weights
深度学习 > 理论基础
#人工智能 #神经网络 #深度学习 #NLP
多头自注意力机制
https://blog.shinebook.net/2025/04/21/人工智能/理论基础/深度学习/多头自注意力机制/
作者
X
发布于
2025年4月21日
许可协议