神经网络的退化
神经网络的退化现象
神经网络的退化（Degradation）是指在深度学习模型中，随着网络层数的增加，模型的性能并没有如预期的那样持续提高，反而出现了性能下降的现象。这种现象与我们的直觉相反，因为理论上更深的网络应该能够捕捉到更复杂的函数关系，从而提高模型的表现。
退化现象通常表现为训练误差和测试误差随着网络层数的增加而增加。即使在训练数据充足且网络能够被充分训练的情况下，退化仍然可能出现。这与过拟合不同，过拟合是指模型在训练数据上表现很好，但在测试数据上表现不佳，而退化则是模型在训练数据上的表现本身就随着层数增加而变差。
神经网络退化的原因
退化的原因尚未完全明了，但通常认为与以下因素有关：
- 梯度消失/爆炸：在深度神经网络中，梯度在反向传播过程中可能会逐渐消失或爆炸，导致网络难以训练。梯度消失使得靠近输入层的层难以学习，而梯度爆炸则可能导致参数更新过大，模型不稳定。
- 参数效率低下：更深的网络意味着更多的参数，但这并不总是意味着更好的性能。有时候，参数的增加并没有被有效利用，反而增加了模型的复杂性和训练难度。
- 优化困难：深度网络的优化是一个非凸问题，随着层数的增加，找到好的局部最小值变得更加困难。
- 信息传递问题：在深度网络中，信息从输入层传递到输出层的过程中可能会逐渐失真，导致网络难以学习到有用的特征。
理论与实际的差距
理论
对于全连接神经网络，下一层神经元个数不少于上一层神经元个数时，理论上深层的神经网络最优解绝对不会差于浅层的神经网络。
假设全连接神经网络有\(L\)层，现在我们将其变为\(L+1\)层的神经网络，也就是在原先\(L\)层的基础上新加入一层。
第\(L\)层的输出为\(x_1, x_2, \cdots, x_n\)，第\(L+1\)层的第\(i\)个神经元的第\(i\)个权重等于1，其余权重和偏置均为0，并且使用ReLU函数作为激活函数，假设第\(L\)层使用的也是ReLU激活函数，也就是第\(L\)层的输出均大于等于0，那么，当第\(L+1\)层的神经元个数等于第\(L\)层的神经元个数时，第\(L+1\)层的输出与第\(L\)层将完全相同；当第\(L+1\)层的神经元个数大于第\(L\)层的神经元个数时，多余的神经元可以学习任意的权重与偏置，第\(L+1\)层神经元除了能输出与第\(L\)层一模一样的信息之外，还能输出更多的信息。
如果不使用ReLU函数，那么我们只需保证第\(L+1\)层的第\(i\)个神经元的第\(i\)个权重\(w_{ii}^{[L+1]}\)满足：\(w_{ii}^{[L+1]}x_i = z_i\)（\(z_i\)为第\(L\)层第\(i\)个神经元线性部分的结果，\(x_i = g(z_i)\)，\(g(\cdot)\)为激活函数），其余权重和偏置均为0，使用与第\(L\)层一样的激活函数，一样能够实现恒等映射。
也就是说，新增的这一层，如果神经元个数大于等于上一层神经元的个数，那么理论上\(L+1\)层的神经网络的最优解不会差于\(L\)层的神经网络。
对于卷积层，使用same卷积，并且过滤器个数不少于输入图像通道数时，理论上更多的卷积层不会使最优解变差。
假设第\(L+1\)层为卷积层，其过滤器的维度为\(n_W\times n_H\times n_c\)，经过学习后，第\(i\)个过滤器的位置为\((\frac{n_w}{2}, \frac{n_H}{2}, i)\)权重为1，其余的权重均为0，该卷积层学习到的偏置结果均为0，使用的激活函数为ReLU函数（之前的卷积层使用的激活函数也为ReLU函数，因此输入的图像的各个元素值均为非负数），若过滤器的个数等于输入图像的通道数时，那么经过该卷积层后，输出的特征图与输入图像完全相同，即输入的信息与输出的信息完全相同；若过滤器的个数大于输入图像的通道数时，多余的过滤器学习到任意的权重，我们不仅能将输入图像完全保留，还能输出更多的信息。
如果不使用ReLU函数，与全连接层类似，我们只需要保证第\(L+1\)层第\(i\)个过滤器的位置为\((\frac{n_w}{2}, \frac{n_H}{2}, i)\)的权重\(w_i\)学习到的值满足：\(w_ix_{x, y, i} = z_{x, y, i}\)（\(x\)表示宽，\(y\)表示高，\(i\)表示第几个通道），其余权重和偏置均为0，使用与第\(L\)层一样的激活函数，一样能够实现恒等映射。
也就是说，新增的这一个卷积层，如果使用same卷积，并且过滤器的个数不少于输入图像通道数时，理论上并不会使得神经网络的最优解变差。
实际
根据实验数据，不管是全连接神经网络还是卷积神经网络，随着网络深度的增加，准确率达到饱和，然后迅速下降，并且这种下降并不是由过拟合引起的，因为其训练误差与测试误差同时增大。
在由权重与偏置为自变量的损失函数中，会有很多很多的极小值，而梯度下降会使得模型在训练集上的误差趋近于其中的一个极小值。更深的神经网络我们可以认为损失函数的最小值会比浅层神经网络代价函数的最小值更小，但是我们很难在这个高维空间中训练到这个最小值，我们更有可能训练得到的模型只是趋近于其中的一个极小值，而这个极小值有可能会比浅层的神经网络训练得到的误差极小值更大，而神经网络层数越多出现这种情况的概率会更大。
从信息传递的角度理解
比如全连接层神经网络，一个神经元接收了上一层所有神经元传递的信息并加工处理后，这个加工后的输出无法还原出它接收的上一层神经元的输出。
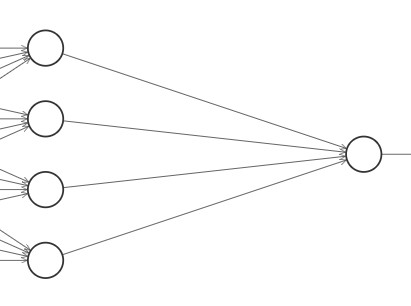
比如上图，右边的神经元会接收左边4个神经元的输出信息，然后进行综合与加工：
\[
z = w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + b = k
\] 通过计算\(\displaystyle\sum_{i=1}^{4}{w_ix_i} + b =
k\)，我们可以得到\(z =
k\)，但我们无法根据\(z =
k\)和\(w_1, w_2, w_3,
w_4\)反推出\(x_1, x_2, x_3,
x_4\)的值。
逆推时，已知的是\(k\)和\(w_1, w_2, w_3, w_4\)，未知的是\(x_1, x_2, x_3, x_4\)，对于\(x_1, x_2, x_3, x_4\)四个未知数，至少需要4个含未知数的等式才能够求出结果，也就是说至少需要4个含未知数的等式，我们才能够将原先的信息还原。
而该层的这个神经元只能够构造出一个含未知数的等式：\(\displaystyle\sum_{i=1}^{4}{w_ix_i} + b = k\)，
那么，我们可以这样认为：信息向前传播一层后，后一层的神经元无法再用综合加工后的信息还原成输入的信息，信息不可逆，出现了信息损失。
我们再回到理论情况：对于全连接神经网络，下一层神经元个数不少于上一层神经元个数时，理论上深层的神经网络最优解绝对不会差于浅层的神经网络。
从信息的角度理解，下一层神经元个数不少于上一层神经元个数时，理论上可以将信息还原。因为这个时候我们能构造的含未知数的等式的个数大于等于输入信息数，也就是大于等于未知数的个数。
对于\(\displaystyle\sum_{i=1}^{4}{w_ix_i} + b = k\)，我们可以表示为： \[ \displaystyle\sum_{i=1}^{4}{w_ix_i} = k - b \] 因为\(b\)与\(k\)均为已知量，为了便于表示，令\(b = k - b\)，则： \[ \displaystyle\sum_{i=1}^{4}{w_ix_i} = b \] 从线性代数的角度，我们可以将构造的这些等式用矩阵来表示： \[ Ax = (a_1, a_2, \cdots, a_n)\left( \begin{matrix} x_1\\\ x_2\\\ \vdots\\\ x_n \end{matrix} \right) = b \] 其中，\(a_1, a_2, \cdots, a_n\)均为列向量： \[ a_i = \left( \begin{matrix} a_{i,1}\\\ a_{i,2}\\\ \vdots\\\ a_{i,m} \end{matrix} \right) \] 对于非齐次线性方程组\(Ax=b\)，有如下定理：
设\(Ax=b\)是\(m\times n\)型非齐次线性方程组，则：
\(Ax=b\)有解\(\Leftrightarrow r(A, b) = r(A)\)
\(Ax=b\)有唯一解\(\Leftrightarrow r(A, b) = r(A) = n\)
因为上一层神经元的输出就是这一层神经元对应非齐次线性方程组的一组解，因此\(Ax=b\)一定有解，即一定满足\(r(A, b) = r(A)\)，
如果这一层能够还原出上一层输出的信息，那么代表\(Ax=b\)有唯一解；如果不能够还原，那么代表\(Ax=b\)有无穷多解。
\(Ax=b\)为\(m\times n\)型非齐次线性方程组，也就是\(m\)行\(n\)列，也就是有\(n\)个变量，\(m\)个等式，也就对应着这一层有\(m\)个神经元，上一层有\(n\)个神经元。
如果能够还原出上一层的信息，则\(r(A) = n\)；如果不能还原出上一层的信息，则\(r(A) < n\)。
而\(A\)为系数矩阵，也就是该层所有神经元的所有权重构成的矩阵，
在全连接神经网络的前向传播中， \[ \begin{aligned} z^{[l]} &= W^{[l]}g(z^{[l-1]}) + b^{[l]}\\\ &= W^{[l]}g\big(W^{[l-1]}g(z^{[l-2]})+b^{[l-1]}\big)+b^{[l]}\\\ &= W^{[l]}g\big(W^{[l-1]}g\Big(W^{[l-2]}g(\cdots)+b^{[l-2]}\big)+b^{[l-1]}\Big)+b^{[l]} \end{aligned} \] 我们需要根据\(z^{[l]} = W^{[l]}g(z^{[l-1]}) + b^{[l]}\)还原出\(g(z^{[l]})\)，即根据\(W^{[l]}g(z^{[l-1]}) = z^{[l]} - b^{[l]}\Leftrightarrow Ax=b\)还原出\(g(z^{[l-1]})\)，假设\(g(\cdot)\)是可逆的，还原出了\(g(z^{[l-1]})\)就还原出了\(z^{[l-1]}\)，
然后我们要根据\(z^{[l-1]} = W^{[l-1]}g(z^{[l-2]}) + b^{[l-1]}\)还原出\(g(z^{[l-2]})\)，依此类推。
我们很难保证所有的\(W^{[i]}\)均满足\(r(W^{[i]}) = n^{[i-1]}\)（\(n^{[i-1]}\)表示第\(i-1\)层神经元的个数），也就是说，我们很难保证每层神经元传播时都没有信息的损失，一旦神经网络层数加深，信息损失的可能性越大，信息损失的程度也越高。
对于卷积神经网络，卷积层输入输出展开后可以看成类似于全连接层但是没有全连接的情况，并且卷积层还有共享权重的情况，这就使得系数矩阵的线性相关性更强（多个神经元对应同一组权重，系数矩阵上会出现多行的值相同的情况），因此卷积层也会导致信息的损失。而池化层，不管是选取平均池化还是最大池化，池化的过程完全不可逆（无法根据平均值确定平均前的各个值，也无法根据最大值来确定其他更小的值），因此池化必然出现信息损失（这也是池化能缓解过拟合的原因）。
在神经网络的加深过程中，前期网络拟合复杂度的提升收益比信息损失带来的负面效益要高，后面区域平衡，然后信息损失带来的负面效益要高于神经网络复杂度提高带来的正面效益。（我们可以认为前面丢失掉的是不重要的信息，越深层的神经网络传递的信息越重要，这时候丢失信息反而得不偿失）
第\(l\)层的线性部分\(z^{[l]}\)经过了很多的系数矩阵\(W^{[l]}\)的乘法，根据定理：
设\(A\)为\(m\times k\)型矩阵，\(B\)为\(k\times n\)型矩阵，则 \[ r(A) + r(B) - k \leq r(AB) \leq \min\{r(A), r(B)\} \]
也就是当两个矩阵相乘时，新矩阵的秩会小于等于原先两个矩阵最小的秩，
根据全连接神经网络的前向传播公式， \[ \begin{aligned} z^{[l]} &= W^{[l]}g(z^{[l-1]}) + b^{[l]}\\\ &= W^{[l]}g\big(W^{[l-1]}g(z^{[l-2]})+b^{[l-1]}\big)+b^{[l]}\\\ &= W^{[l]}g\big(W^{[l-1]}g\Big(W^{[l-2]}g(\cdots)+b^{[l-2]}\big)+b^{[l-1]}\Big)+b^{[l]} \end{aligned} \] 对于\(z^{[l]} = W^{[l]}g(z^{[l-1]})+b^{[l]}\)， \[ r\Big(W^{[l]}g(z^{[l-1]})\Big) \leq \min\Big\{r(W^{[l]}), r\Big(g(z^{[l-1]})\Big)\Big\} \] 因为神经网络的前向传播，\(z^{[l]} = W^{[l]}g(z^{[l-1]})+b^{[l]}\)一定有解，因此， \[ r\Big(W^{[l]}g(z^{[l-1]})+b^{[l]}\Big) = r\Big(W^{[l]}g(z^{[l-1]})+b^{[l]},z^{[l]}\Big) \leq n^{[l-1]} \] 就算\(W^{[l]}g(z^{[l-1]})\)和\(b^{[l]}\)的秩均为\(n^{[l-1]}\)，它们相加的秩也不一定为\(n^{[l-1]}\)，有可能会更小。
根据上述公式和结论，我们发现，逐层传播后，\(z^{[l]}\)经过了众多的矩阵相乘与相加，因此\(z^{[l]}\)的秩可能会随着\(l\)增大而越来越小，矩阵\(z^{[l]}\)的秩减小导致其内部列向量极大无关组的向量个数会减小，矩阵内部列向量线性相关性会变强，传播的信息重复性增大，损失了不重复的一些信息，导致神经网络的退化。
对于卷积神经网络，卷积层输出与输入平铺后同理，池化层：在使用最大池化时，可能过滤器在几个位置选取的最大值都相同，导致信息重复；在使用平均池化时，因为图像大部分时候都是渐变的，相邻的输出的值也很可能相差很小，导致信息重复。实际上，为了少许的平移不变性，必然要付出信息重复的代价。
神经网络退化的解决方案
使用快捷连接（Shortcut Connection），比如ResNet