神经网络的激活函数
为什么需要选择非线性的函数作为激活函数
如果我们选择线性的激活函数,也就等价于将神经元第二步的非线性计算删除,即: \[ a = g(z) = z \] 对于第\(l\)层神经网络: \[ \left\{ \begin{aligned} &Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]}\\\ &A^{[l]} = g(Z^{[l]}) = Z^{[l]} \end{aligned} \right. \] 则: \[ \begin{aligned} Z^{[l]} &= W^{[l]}A^{[l-1]} + b^{[l]}\\\ &= W^{[l]}(W^{[l-1]}A^{[l-2]}+b^{[l-1]})+b^{[l]}\\\ &= W^{[l]}W^{[l-1]}A^{[l-2]}+(W^{[l]}b^{[l-1]}+b^{[l]}) \end{aligned} \] 令 \[ \left\{ \begin{aligned} &W' = W^{[l]}W^{[l-1]}\\\ &b' = W^{[l]}b^{[l-1]}+b^{[l]} \end{aligned} \right. \] 则: \[ Z^{[l]} = W'A^{[l-2]}+b' \] 也就是说,第\(l-2\)层到第\(l\)层,等价于第\(l-1\)层调整参数后到第\(l\)层,依次类推,如果激活函数都是线性的,整个神经网络都等价于一个一层的神经网络,即只有输入层和输出层。
因此,我们需要选用非线性的激活函数
当然,输出层的激活函数可以是线性的,因为其后面不再有神经网络了。
常见的激活函数
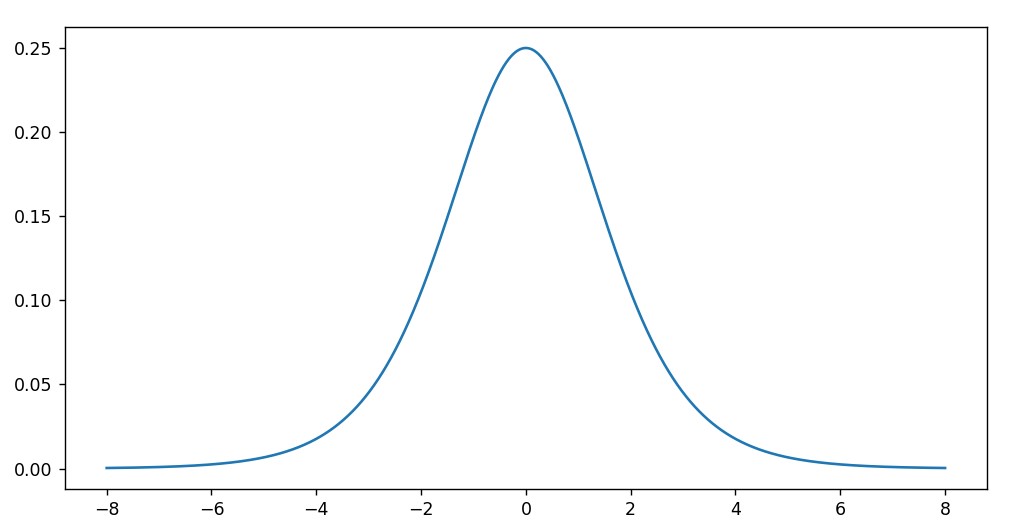
sigmoid激活函数
函数与导数
函数
\[ a = g(z) = \frac{1}{1+e^{-z}} \]

导数
\[ a = g(z) = \frac{1}{1+e^{-z}} \]
\[ g'(z) = \frac{1}{1+e^{-z}} - \bigg(\frac{1}{1+e^{-z}}\bigg)^2 = g(z)-g(z)^2 = g(z)[1-g(z)] \]
因此: \[
g'(z) = a(1-a)
\] 
优点
- sigmoid函数的输出结果在\((0,1)\)之间,可以用于分类(作为输出层的激活函数)
缺点
- sigmoid函数的导数最大值也就0.25,如果神经网络层数较多,很容易造成梯度消失
- 当\(z\)的值较大或较小时,sigmoid的导数值会非常小,即使只有一个隐藏层,训练效果也不好
- 导数值过小,学习速度慢
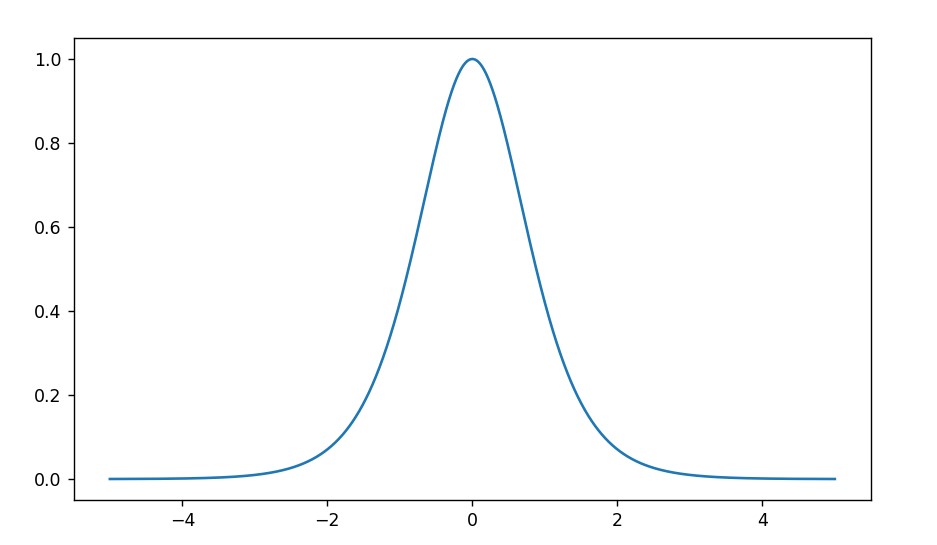
双曲正切函数(tanh函数)
函数与导数
函数
\[ a = g(z) = \tanh(z) = \frac{e^z-e^{-z}}{e^z+e^{-z}} \]

导数
\[ a = g(z) = \tanh(z) \]
\[ g'(z) = 1 - (\tanh(z))^2 = 1 - g(z)^2 \]
因此: \[
g'(z) = 1 - a^2
\] 
优点
- 相比于sigmoid函数,\(\tanh(z)\)具有居中数据的效果,也就是数据平均值接近0而不是0.5,优于sigmoid函数
- 相比于sigmoid函数的导数,\(\tanh(z)\)的导数值在相同情况下更大,在相同层数的神经网络下,发生梯度消失的可能性比用sigmoid函数更小
缺点
- 能够支持的神经网络深度还是不够,层数一多依旧会出现梯度消失的情况
- 当\(z\)比较大或者比较小的时候,导数值很小,学习速度会变慢,效果不好
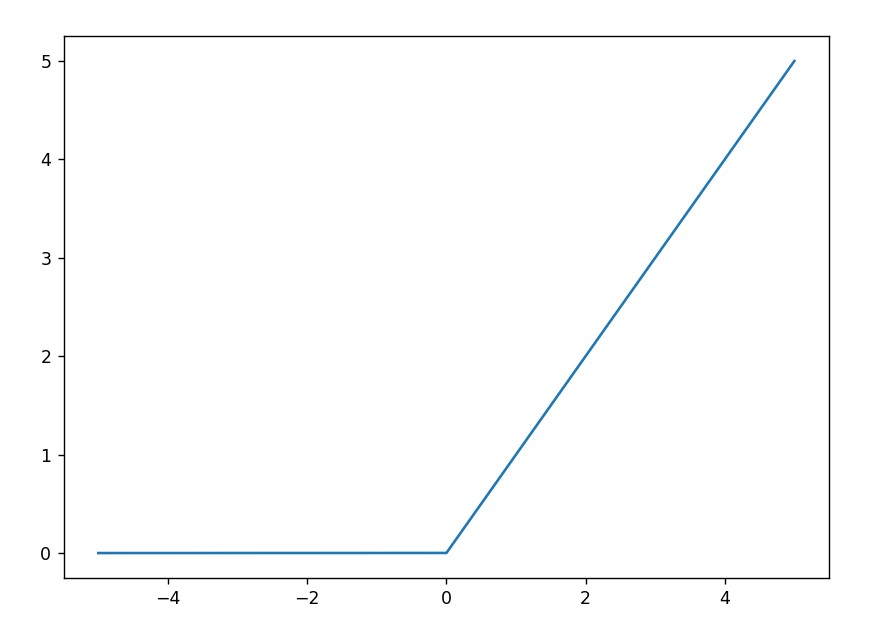
ReLU函数
ReLU函数,叫做线性整流函数、整流线性单元、整流线性单元函数,ReLU是最常用的激活函数
函数与导数
函数
\[ a = g(z) = \max(0,z) \]
即: \[
a = g(z) = \left\{
\begin{aligned}
1\quad\quad z > 0\\\
0\quad\quad z \leq 0
\end{aligned}
\right.
\] 
导数
\[ a = g(z) = \max(0,z) \]
\[ g'(z) = \left\{ \begin{aligned} &1\quad\quad z > 0\\\ &0\quad\quad z < 0 \end{aligned} \right. \]
注意:当\(z=0\)时,ReLU函数不可导,但是我们可以令其为0或1

优点
- 在\(z>0\)时,ReLU导数始终为1,不会造成梯度消失,神经网络的学习速度会比sigmoid和\(\tanh\)的学习速度更快
- 在\(z>0\)时,ReLU导数不会随着\(z\)变化,学习速度稳定,不会因为\(z\)过大而导致导数过小
缺点
- 当\(z \leq 0\)时,ReLU函数和导数均为0,这个神经元不能再更新参数,也就是该神经元不再学习了(Dead ReLU问题,“神经元死亡”,也就是神经元不再被激活,参数不再更新)
Leaky ReLU
函数和导数
函数
\[ a = g(z) = \max(\lambda z, z) \]
其中, \[ \lambda \in (0,1) \] 一般情况下,\(\lambda\)的值都会设置得比较小,比如:\(\lambda = 0.01\)

导数
\[ a = g(z) = \max(\lambda z, z)\quad \lambda \in (0,1) \]
\[ g'(z) = \left\{ \begin{aligned} &1\quad\quad z > 0\\\ &\lambda\quad\quad z < 0 \end{aligned} \right. \]
注意:当\(z=0\)时,Leaky ReLU函数不可导,但是我们可以令其为\(\lambda\)或1
优点
- Leaky ReLU能够解决ReLU当\(z<0\)时函数和导数均为0的情况,这样保留了负轴的值,使得负轴的值不会全部丢失
尽管理论上Leaky ReLU比ReLU更优,但目前在实践中没有充分的证据表明Leaky ReLU总是比ReLU好
PReLU
Leaky ReLU是PReLU的特殊版本
函数和导数
函数
\[ a = g(z) = \left\{ \begin{aligned} &z\quad\quad &z > 0\\\ &\lambda z\quad\quad &z \leq 0 \end{aligned} \right. \]
- 如果\(\lambda = 0\),则PReLU函数变为ReLU函数
- 如果\(\lambda \in (0,1)\),则PReLU函数变为Leaky ReLU函数
导数
\[ a = g(z) = \left\{ \begin{aligned} &z\quad\quad &z > 0\\\ &\lambda z\quad\quad &z \leq 0 \end{aligned} \right. \]
\[ g'(z) = \left\{ \begin{aligned} &1\quad\quad z > 0\\\ &\lambda\quad\quad z < 0 \end{aligned} \right. \]
注意:当\(z=0\)时,PReLU函数不可导,但是我们可以令其为\(\lambda\)或1
ELU
函数和导数
函数
\[ a = g(z) = \left\{ \begin{aligned} &z\quad\quad &z > 0\\\ &\alpha(e^{x}-1)\quad&z \leq 0 \end{aligned} \right. \]

导数
\[ a = g(z) = \left\{ \begin{aligned} &z\quad\quad &z > 0\\\ &\alpha(e^{x}-1)\quad&z \leq 0 \end{aligned} \right. \]
\[ g'(z) = \left\{ \begin{aligned} &1\quad\quad &z>0\\\ &\alpha e^x\quad &z\leq 0 \end{aligned} \right. \]
优点
- 除了兼具Leaky ReLU的优点之外,ELU函数及其导数在\(z<0\)时具有软饱和性
- 右侧线性部分使得ELU能够缓解梯度消失,左侧软饱和性能够让ELU对输入变化或噪声更具有鲁棒性
- ELU通过减少偏置偏移的影响,使正常梯度更接近于单位自然梯度,从而使均值向0加速学习
尽管理论上ELU算法更优,但实际应用上并没有多大体现。