残差网络(ResNet)
ResNet
ResNet(残差网络)是由来自Microsoft Research的4位学者(何凯明、张翔宇、任少卿、孙剑)提出的,获得了2015年ImageNet竞赛中分类任务第一名与目标检测第一名。
神经网络的退化
在我们原先的印象中,神经网络层数越多、神经元的个数越多,神经网络就能够拟合更加复杂的函数,能够学习更加复杂的内容,表达的效果也应该更好。
但在真正的实验数据中,当网络达到一定深度后,随着网络层数的增加,神经网络会发生退化的现象,也就是说:随着网络层数的增加,训练集的代价函数逐渐下降,然后趋于饱和,当我们再增加神经网络的深度的话,训练集的代价函数反而会增大。因为是训练集的代价函数增大,因此并不是过拟合的现象,过拟合训练集的代价函数依然会减小。
当神经网络发生退化时,浅层的神经网络反而能够实现比深层神经网络更好的训练效果。

神经网络退化的解决方案
如果浅层的神经网络学习的效果比深层的神经网络更好,那么我们期望深层的神经网络不再学习,而是直接输出浅层神经网络的结果,这样至少能保证神经网络的性能不会更差。
比如,现在有\(N\)层的神经网络,我们给这个神经网络再加入两层(加入\(N+1\)层和\(N+2\)层),新的\(N+2\)层的神经网络或许会比原本\(N\)层的神经网络拟合效果更好,但也有可能更差,为了避免更差的这种情况出现,我们可以将第\(N\)层的输出直接当做第\(N+2\)层的输出。
但这也导致了一个问题,就是这么做等于没有加入后面两层神经网络,反而更加浪费算力,神经网络也失去了表达能力更好的潜在可能性。
因此,我们可以综合考虑第\(N+2\)层的输出和第\(N\)层的输出。
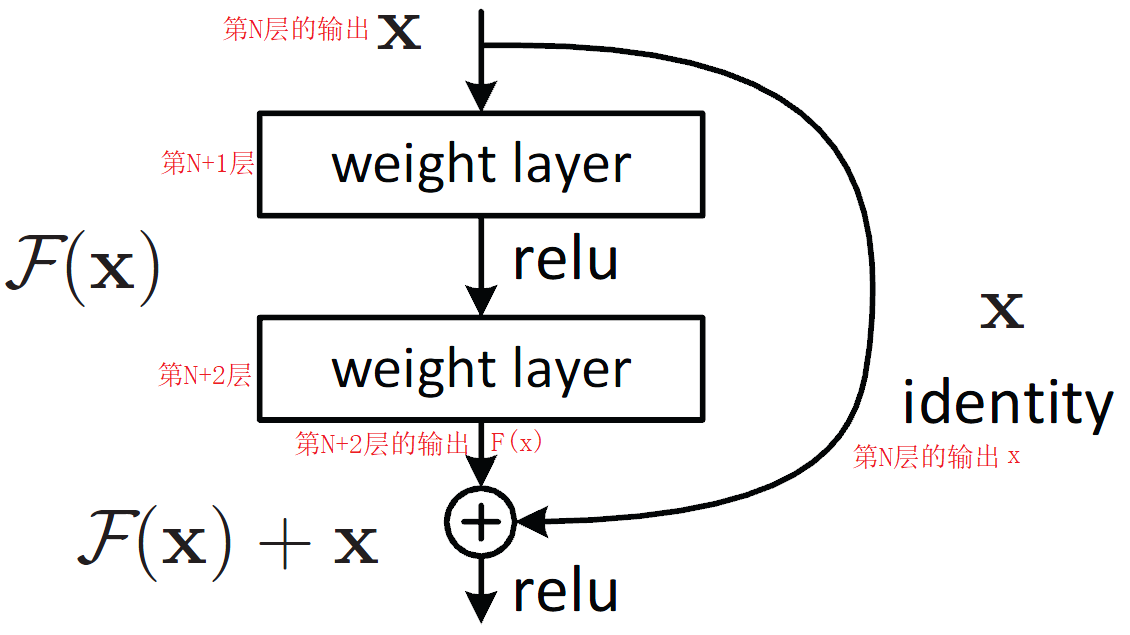
如上图,将第\(N\)层的输出与第\(N+2\)层的输出连起来,其中第\(N\)层的输出为\(x\),第\(N+2\)层的输出是第\(N\)层输出经过处理的结果,可以认为是关于第\(N\)层输出\(x\)的函数:\(\mathcal{F}(x)\),我们将第\(N\)层的输出和第\(N+2\)层的输出加起来,得到\(H(x) = \mathcal{F}(x) + x\),
那么,\(\mathcal{F}(x) = H(x) - x\),如果第\(N\)层的输出优于第\(N+2\)层的输出,那么最终我们可以训练出\(\mathcal{F}(x) = 0\),也就实现了直接输出第\(N\)层的结果,使得\(N+2\)层神经网络网络的训练效果至少不会比\(N\)层的神经网络差。
如果\(N+2\)层的输出结果会好于\(N\)层的输出结果,那么\(\mathcal{F}(x)\neq 0\),也就是说,我们可以用这种结构将神经网络训练得更好,至少不会比浅层的神经网络效果差。
在上面的这个模块中,\(x\)是第\(N\)层的输出,也就是这个模块的输入特征,可以认为是观测值(拟合的结果不一定准确,因此不是真实值,可以认为是观测的结果),\(H(x)\)是这个模块的输出结果,可以认为是预测值,\(\mathcal{F}(x)\)为\(H(x) - x\),也就是预测值减去观测值,而预测值减观测值的结果是残差,因此,\(\mathcal{F}(x)\)表示残差,因此,在这个模块中,学习训练的其实是残差,而这个模块也被称为残差结构(residual结构),或者残差块(Residual block)


在残差块中,\(\mathcal{F}(x)\)并不是该结构中最后一个神经层的完整输出结果,它并没有经过激活函数,而是在和\(x\)相加后再通过ReLU激活函数。而该结构的输入\(x\)则是之前神经层的完整输出结果(经过了激活函数),假设该结构的两个神经层分别为第\(l+1\)层和第\(l+2\)层,输出\(x\)的神经层为第\(l\)层,\(z^{[l]}\)为第\(l\)层的线性结果,\(a^{[l]}\)为第\(l\)层的输出结果,则\(a^{[l]} = g(z^{[l]})\),\(g(z^{[l]})\)为激活函数。那么, \[ a^{[l+2]} = g(a^{[l]} + z^{[l+2]}) \] 在残差块中,连接输入与输出的“捷径”(也就是\(x\))被称为shortcut。
在残差块中,因为\(x\)和最后一层神经元的输出\(\mathcal F(x)\)需要相加才会得到预测结果\(H(x)\),因此,在卷积网络中,\(x\)需要与\(\mathcal F(x)\)对应的图像需要有相同的维度,否则我们无法将二者的矩阵或立方体对应的位置相加。

因此,在残差块的主分支中,我们可以选用same卷积,每个卷积层过滤器的个数与输入图像通道数相同,在残差块中不使用池化层。
如果在主分支卷积后的输出图像维度与残差块的输入图像维度不同,我们可以使用\(1\times1\)卷积来使二者图像的通道数相同,通过调整步幅(stride)来使得二者图像的高与宽相同。
残差网络
在残差网络中,残差块有两种:

左边是针对ResNet-18/34的残差块(BasicBlock),也就是对应18层或34层神经网络的残差块;右边是针对ResNet-50/101/152的残差块(bottleneck),也就是对应50层或101层或152层的神经网络。


论文中两种残差块所拥有的超参数在上面两张图中已经展示。因为输入图像和输出图像维度不一致,因此在shortcut中使用了\(1\times1\)卷积进行了升维/降维操作。
这个时候,我们可以认为原本直接映射到输出中的\(x\)变为了关于\(x\)的函数\(h(x)\),此时: \[ H(x) = h(x) + \mathcal F(x) \] \(\mathcal F(x)\)并不是只是关于\(x\)的函数,其还与残差块主分支中过滤器的权重有关,因此可以表示为\(\mathcal F(x, W)\),当然,卷积操作后一般要加入偏置bias,因此可以表示为\(\mathcal F(x, W, b)\),如果是对于第\(l\)个残差块,那么函数可以表示为\(\mathcal F(x_l, W_l)\)或者\(\mathcal F(x_l, W_l, b_l)\),而我们这里使用\(\mathcal F(x_l)\),只是一种简写方式
把整个残差块当成一个整体,那么对于第\(l\)个残差块,有: \[ \begin{aligned} &y_l = H(x) = h(x_l) + \mathcal F(x_l)\\\ &x_{l+1} = f(y_l) \end{aligned} \] 其中,\(f(\cdot)\)是激活函数,一般选用ReLU函数。在卷积神经网络中,我们可以认为输入输出的图像的元素值均为非负数,那么,\(f(\cdot)\)为直接映射,也就是说, \[ x_{l+1} = y_l = H(x) = h(x_l) + \mathcal F(x_l) \] 在不考虑升维/降维操作时,也就是均进行same卷积且过滤器个数等于输入图像通道数时,在shortcut中我们无需使用\(1\times1\)卷积,\(h(\cdot)\)是直接映射,此时, \[ x_{l+1} = x_l + \mathcal F(x_l) \] 对于一个更深的层\(L\),其与\(l\)层的关系可以表示为: \[ \begin{aligned} x_L &= x_{L-1}+\mathcal F(x_{L-1})\\\ &= x_{L-2} + \mathcal F(x_{L-2})+\mathcal F(x_{L-1})\\\ &= \cdots\cdots\\\ &= x_l + \displaystyle\sum_{i = l}^{L-1}{\mathcal F(x_i)} \end{aligned} \] 因此,对于残差网络而言,\(L\)层可以表示为任意一个比它浅的\(l\)层和它们之间的残差部分之和,而每个残差块所学习的就是各自的残差。
根据链式法则,损失函数\(\varepsilon\)关于\(x_l\)的梯度可以表示为: \[ \begin{aligned} \frac{\partial \varepsilon}{\partial x_l} &= \frac{\partial \varepsilon}{\partial x_L}\cdot\frac{\partial x_L}{\partial x_l} \\\ &= \frac{\partial \varepsilon}{\partial x_L}\cdot\frac{\partial \Bigg(x_l + \displaystyle\sum_{i = l}^{L-1}{\mathcal F(x_i)}\Bigg)}{\partial x_l} \\\ &= \frac{\partial \varepsilon}{\partial x_L}\bigg(1 + \frac{\partial}{\partial x_l}\displaystyle\sum_{i=l}^{L-1}{\mathcal F(x_i)}\bigg)\\\ &= \frac{\partial \varepsilon}{\partial x_L} + \frac{\partial \varepsilon}{\partial x_L}\frac{\partial}{\partial x_l}\displaystyle\sum_{i=l}^{L-1}{\mathcal F(x_i)} \end{aligned} \]
- \(\frac{\partial \varepsilon}{\partial x_L}\)表明损失函数\(\varepsilon\)对第\(L\)层输出结果\(x_L\)的导数可以直接传递到任何一个比它浅的\(l\)层
- 残差网络能够有效缓解梯度消失问题,原因如下:
残差网络从第\(L\)层反向传播到第\(l\)层的梯度为\(\frac{\partial \varepsilon}{\partial x_L} + \frac{\partial \varepsilon}{\partial x_L}\frac{\partial}{\partial x_l}\displaystyle\sum_{i=l}^{L-1}{\mathcal F(x_i)}\),而MLP神经网络从第\(L\)层反向传播到第\(l\)层的梯度为$W{[l+1]T}(W{[l+2]T}(W{[l+3]T}((W{[L]T}g'(Z^{[L-1]})))g'(Z{[l+2]}))g'(Z{[l+1]}))g'(Z^{[l]}) \(,我们可以发现,普通的神经网络从第\)L\(层到第\)l\(层的反向传播需要不断连乘,这样极容易导致指数效应,如果小于1的数累乘会出现梯度消失,如果大于1的数累乘会出现梯度爆炸,但残差网络从第\)L\(层到第\)l\(层的反向传播不需要不断累乘(公式中最多三连乘),并且将\)L\(层到\)l\(层的残差进行了累加,并且还加上了损失函数对\)x_L\(的梯度\)$,在这么多作用的结果下,残差网络可以有效缓解梯度消失的问题。
根据\(\frac{\partial \varepsilon}{\partial x_L}\bigg(1 + \frac{\partial}{\partial x_l}\displaystyle\sum_{i=l}^{L-1}{\mathcal F(x_i)}\bigg)\),如果在残差网络中出现梯度消失,所需要的条件是比较苛刻的:\(\frac{\partial \varepsilon}{\partial x_L}\)需要趋近于0,或者\(\frac{\partial}{\partial x_l}\displaystyle\sum_{i=l}^{L-1}{\mathcal F(x_i)}\)趋近于-1
根据上述两个结论:1. \(L\)层可以表示为任意一个比它浅的\(l\)层和它们之间的残差部分之和 2. \(L\)层的梯度可以直接传递到任何一个比它浅的\(l\)层,我们可以得到结果:信息可以非常畅通地在高层和低层之间相互传导,不容易出现损失。
如果\(h(\cdot)\)不是直接映射,假设\(h(x_l) = \lambda_lx_l\),那么: \[ \begin{aligned} x_L &= \lambda_{L-1}x_{L-1} + \mathcal F(x_{L-1})\\\ &= \lambda_{L-1}\lambda_{L-2}x_{L-2} + \lambda_{L-1}\mathcal F(x_{L-2})\\\ &= \cdots\cdots\\\ &= \Big(\displaystyle\prod_{i=l}^{L-1}{\lambda_i}\Big)x_l + \displaystyle\sum_{l}^{L-1}{\mathcal{\hat F}(x_i)} \end{aligned} \] 其中, \[ \mathcal {\hat F}(x_i) = \Big(\displaystyle\prod_{j=i+1}^{L-1}\lambda_j\Big)\mathcal F(x_i) \] 由此可见,如果\(\lambda_i > 1\),很有可能发生梯度爆炸;如果\(0 < \lambda_i < 1\),很有可能发生梯度消失。这两种情况都会阻碍神经网络的训练。
因此\(\lambda=1\)是最优的选择,这种情况对应的是直接映射。
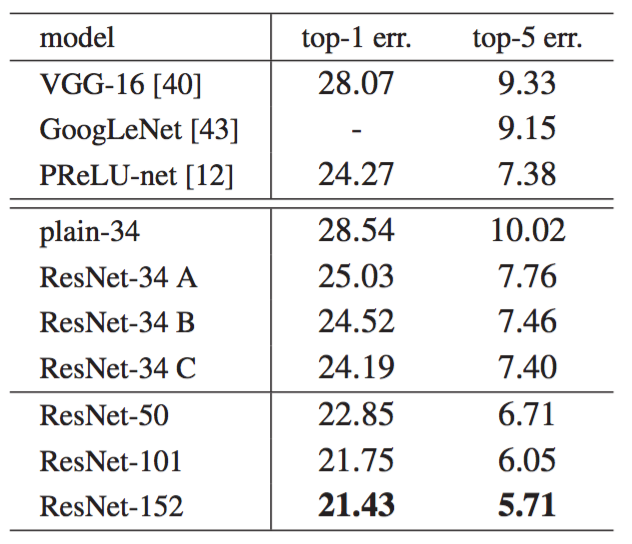
上图中的ResNet-34有三种分类:
零填充shortcut connection(快捷连接)来增加维度(使得\(x\)与\(\mathcal F(x)\)维度相同),所有的shortcut connection是没有参数的
投影shortcut用来增加维度,其他的shortcut connection是恒等的
所有的shortcut都是投影
上表表明所有的三个选项都比对应的简单网络好很多。选项B比A略好。我们认为这是因为A中的零填充确实没有残差学习。选项C比B稍好,我们把这归因于许多投影shortcut connection引入了额外参数。但A/B/C之间的细微差异表明,投影shortcut connection对于解决退化问题不是至关重要的。使用B而不是使用C有利于减少内存/时间复杂性和模型大小。
注:引入投影:对于\(y = H(x) = \mathcal F(x, W_i) + x\),因为\(\mathcal F(x, W_i)\)必须与输入图像最终维度是相等的,因此我们通过快捷连接执行线性投影\(W_s\)来匹配维度:\(y = H(x) = \mathcal F(x, W_i) + W_sx\)